
위의 그림은 3개의 학습 데이터에 대해 임의의 가중치 W 행렬을 가지고 예측한 10개의 클래스 스코어이다.
굵게 표시된 스코어를 보면 이 보다 스코어가 더 높은 것도, 낮은 것도 볼 수 있다.
예를 들어 고양이 이미지에서 고양이 클래스의 스코어가 가장 높기를 기대하지만
예측된 점수는 2.9로 그리 높지 않으며 개구리가 3.78로 더 높다.
이 스코어를 보면 이 분류기는 그리 좋지 않다.
우리는 정답 클래스, 여기서는 고양이가 가장 높은 점수를 예측하는 분류기를 원한다.
동일한 가중치 W를 가지고 다른 이미지를 보자.
자동차 이미지에서는 자동차 점수가 6.04 가장 높다.
자동차에 대한 분류 성능이 괜찮은 가중치 W라고 볼 수 있다.
개구리 이미지에서 개구리 점수는 -4.34로 다른 점수들보다 훨씬 낮다.
이렇게 스코어를 확인하고 분석하는 방법은 좋지 않다.
어떤 알고리즘을 만들고 어떤 가중치 W가 가장 좋은지, 나쁜지를 결정하기 위해서는
가중치 W가 좋은지 나쁜지에 대해 정량화할 방법이 필요하다.
가중치 W를 입력으로 받아 각 스코어를 확인하고,
이 가중치 W가 얼마나 좋은지 나쁜지를 정량적으로 측정하는 것이 바로 손실함수(Loss Function)이다.
그리고 가중치 행렬 W가 될 수 있는 모든 경우의 수에 대해서
'가장 덜 나쁜' W가 무엇인지를 찾아야 한다.
이 과정이 최적화(Optimization)이다.

여기서는 3개의 트레이닝 이미지와 3개의 클래스를 사용한다. 10개는 너무 많으니까.
점수를 보면 고양이는 잘 분류하지 못했고, 자동차는 잘 분류했고, 개구리는 점수가 최악이다.
이를 손실함수로 공식화해보자.
트레이닝 데이터 x가 있다. x는 알고리즘의 입력으로 image classification 문제라면 이미지가 될 것이다.
레이블 데이터 y가 있다. y는 image classification 문제라면 해당 이미지에 대한 레이블이 될 것이다.
10개의 클래스라면 레이블 y는 1에서 10사이의 정수값이 된다. 프로그래밍 언어에 따라 0~9일수도 있다.
어째든 y라는 정수값은 입력 이미지 X에 대한 정답 카테고리를 의미한다.
앞서 예측함수 f를 정의했다.
입력 이미지 x와 가중치 행렬 w를 입력으로 받아서 새로운 테스트 이미지에 대해 y를 예측하는 것이다.
위에 말한대로 cifar-10의 경우 y는 10개가 된다.
손실함수 Li를 정의해보자.
Li는 예측함수 f와 정답값 y를 입력으로 받아 트레이닝 샘플을 얼마나 예측하는지 정량화한다.
최종 loss인 L은 데이터셋에서 각 N개의 샘플들의 loss의 평균이 된다.
이러한 L 함수는 image classification 문제에 국한되지 않는 아주 일반적인 공식이다.
좀 더 나아가 다른 딥러닝 알고리즘을 살펴보자면, 어떤 알고리즘이던 가장 일반적으로 진행되는 일은,
어떤 x와 y가 존재하고, 가중치 w가 얼마나 좋을지를 정량화하는 손실 함수를 만드는 것이다.
구체적으로 한 손실 함수를 살펴보자. 이 손실 함수는 image classification에 아주 적합하기도 하다.
바로 multi-class SVM loss이다.

이 loss는 힌지 로스(hinge loss)라고도 불린다.
위에 언급한 기본적인 loss와 비슷하지만 조건이 생겼다.
sj는 '정답이 아닌' 클래스의 스코어이다.
syi는 '정답' 클래스의 스코어이다.
조건을 보면 if 정답 클래스 스코어(syi)가 정답이 아닌 클래스 스코어(sj) + safety margin(여기서는 1) 값보다
크거나 같으면 loss가 0이 된다.
그리고 위의 조건이 아니면(otherwise),
정답이 아닌 클래스 스코어(sj) - 정답 클래스 스코어(syi) + safety margin(여기서는 1) 값을 loss로 한다.
만약 정답인 클래스 스코어가 정답이 아닌 클래스 스코어 + safety margin(여기서는 1)보다 크면 loss가 0이 되며,
loss가 0이라는 것은 매우 좋다는 것이다.
syi가 sj보다 충분히 커야 잘 분류했다고 할 수 있다.
그런데 근소한 차이로 분류한다면 새로운 테스트 이미지에서 틀릴 경우가 생길 것이다.
safety margin을 포함해서 더 큰 차이로 분류했을때를 Loss가 0인 경우로 정의한다.

그래프로 그리면 위와 같은 그림이 된다.
이 모양이 경첩처럼 생겼다고 해서 hinge loss라고 이름이 붙여졌다.
다음 예시를 보자.

SVM loss는 앞서 조건들에 의해 오른쪽 파란색 박스와 같이 정의된다.
고양이 클래스를 보자.
우선 정답이 아닌 클래스(자동차)의 점수(sj)를 살펴보면,
자동차 점수가 5.1, 고양이 점수가 3.2로 자동차가 높다.
5.1 - 3.2 + 1 = 2.9가 된다.
또 다른 정답이 아닌 클래스(개구리)의 점수(sj)를 살펴보면,
개구리 점수가 -1.7, 고양이 점수가 3.2로 고양이가 높다.
-1.7 - 3.2 + 1 = -3.9
이는 0 보다 작으므로 loss는 0이 된다.
이들의 합(시그마)을 구해야하기 때문에 더해준다.
2.9 + 0 = 2.9 가 고양이 클래스의 loss가 된다.
자동차 클래스와 개구리 클래스에도 동일하게 적용해보자.


자동차 클래스는 명확합니다.
왜냐하면 자동차가 아닌 클래스(고양이, 개구리) 둘 다 + 1(safety margine)을 해도
자동차 스코어를 넘지 못하기 때문이다. 그럼 loss가 전부 0이 나온다.
개구리 클래스를 보자.
개구리 loss를 구하니까 12.9가 나온다. 고양이 클래스는 2.9 였는데 개구리는 12.9가 나온다.
고양이 클래스에서 고양이 점수가 개구리보단 점수가 높았기 때문에 loss가 비교적 낮은것이다.
개구리를 분류하는 것에 있어서 12.9만큼 안좋다는 의미이며, 고양이 분류보다 훨씬 안좋다고 볼 수 있다.

최종적으로 loss를 다 더하고 (2.9 + 0 + 12.9) 클래스가 3개니 3으로 나눠서 평균을 구한다.
그렇게 계산된 5.27이 최종 loss가 된다.

만약 자동차의 점수를 살짝만 바꾸면 어떻게 될까?
예를 들어 자동차 클래스에서 자동차 점수가 -1이 되어서 3.9가 됐다고 가정해보자.
그래도 loss는 0으로 변함없을 것이다.
왜냐하면 고양이(1.3)에 1을 더해도 개구리(2.0)에 1을 더해도 자동차가 더 높기 때문이다.
여기서 SVM hinge loss의 특성을 알 수 있다.
데이터에 민감하지 않다는 것이다. 점수가 몇 점인지는 관심이 없다.
단지 정답 클래스의 점수가 정답이 아닌 클래스의 점수보다 높은가에만 포커스를 두고 있다.

두번째 질문으로 loss 최소/최대는 무엇일까?
loss의 최소는 0이 된다. 0 보다 작으면 0이 max값으로 loss가 되기 때문이다.
최대값은 무한대가 된다.

만약 초기 W가 매우 작아서 스코어가 0에 가까워지면 loss는 어떻게 될까?
스코어가 0에 가까워지면 safety margin(여기서는 1)만 남을거고
각 로스는 1+1=2가 될 것이다. 3개의 클래스니 (2+2+2) / 3 = 2가 나온다.
클래스가 10개라면 (9+9+9... ) / 10 = 9가 될 것이다.
결국 로스는 클래스 개수 - 1이 된다.
이건 디버그 용도로 많이 사용된다.
가중치 W를 0으로 해주면 loss가 클래스 개수 - 1이 잘 나오는지 검사해보는 것이다.
이걸 sanity check라고도 부른다.

4번째 질문으로 지금까지 우리는 정답 클래스의 점수는 제외시켜 loss를 계산했는데, 왜 제외시킬까?
만약 정답 클래스 점수를 포함해서 계산하면 어떻게 될까?
고양이 클래스에서 3.2 - 3.2 + 1 = 1 이렇게 되고, 자동차, 개구리 또한 마찬가지이다.
그럼 평균이 1 증가하는 효과와 마찬가지가 된다.
우리는 최종 loss가 0이 되길 바란다. 하지만 이렇게 되면 1이 제일 좋은 loss가 된다.

5번째 질문으로 만약 sum대신 mean을 사용하면 어떻게 될까?
로스를 더해서 해당 클래스의 loss라고 정의하는 것 대신
평균을 낸다면 loss의 스케일만 작아질 뿐이다. 때문에 별차이 없게 된다.

만약 제곱을 하면 어떻게 될까?
이때는 loss가 다르게 된다. 일단 제곱을 하게 되면 non-linear하게 된다.
제곱을 해서 구하는 방법을 squared hinge loss라고 한다.
때에 따라 잘 동작될 수 있다.
왜냐하면 hinge loss 그래프에서 직선이 아닌 곡선(제곱승)으로 올라가기 때문이다.
그래서 '매우 매우 안좋다' 혹은 '매우 매우 좋다'를 볼때 유용할 수 있다.
하지만 일반적으로는 제곱을 사용하지 않는다.

여기에 또 하나의 문제가 있다.
우리가 최적의 가중치 W를 찾았다고 하면 이 W는 unique한 값일까?
정답은 아니다.
가중치에 2배를 해도 역시 loss는 0을 갖게 된다.

가중치에 2배를 직접 계산을 하면 위의 그림과 같다.
마찬가지로 loss가 0이 되는것을 볼 수 있다.
즉, W는 여러개가 될 수도 있다는 점이다.

W가 여러개 있을 수 있는것이 어떻게 문제가 될까?
우리는 train 보다 test에 관심이 더 크다. 새로운 값에 대해 '예측'하고 싶은 것이다.
하지만 여지껏 가중치 w는 트레이닝셋에 맞추게 진행했다.
그래서 가중치 W는 트레이닝셋에 맞춰졌다.
이 가중치 W가 테스트셋에도 맞춰져 있을까? 아니다.
W는 unique하지 않기 때문에 테스트셋에는 해당 W가 안좋을수 있다.
위의 그림을 보면 파란색 선으로 W를 구했다고 가정하자.
새로운 초록색 샘플이 들어왔을때 잘 예측할 수 있을까? 그렇지 못하고 정확도가 낮을 것이다.
이를 과적합(overfitting)이라고 한다.
파란색 선보다 초록색 선이 낫다는 것이다.
즉, 테스트셋에도 알맞은 W를 찾아야한다.
그래서 수식의 오른쪽에 regularization 텀이 온다.
data loss는 트레이닝 입장에 있고 regularization은 테스트 입장에 있다.
만약 트레인셋에만 맞는 가중치 W를 학습하려고 할때 regulaization은 어느정도 패널티를 부여한다.
입력이 복잡하기 때문에 가중치 W도 고차원으로 학습하려는 경향이 있다.
이에 대해 패널티를 부과하는 것이다.
occam's razor는 과학계에서 사용하는 말이다.
어떤 가설이 세울때 단순한게 더 좋다는 의미를 가진다.

L1 regularization을 살펴보자.
loss function에 해당하는 부분은 기존 loss를 나타낸다.
때문에 기존 loss에 가중치의 절대값만큼의 패널티를 달아주는것과 같다.
이는 cost를 더 커지게 만들어서 가중치 w를 과도한 변화를 막는다고 볼 수 있다.
이상치에 대한 W를 0으로 만들어버리는 특징이 있다.
여기서 람다는 regularization strength로 하이퍼파라미터이다.
이것이 작아질수록 약한 정규화가 된다.
이렇게 L1 regularization을 사용하는 선형 회귀 모델을 Lasso model이라고도 한다.
L2 regularization을 살펴보자.
마찬가지로 기존 loss에 regularization 텀이 붙는 형태이다.
다른 점은 가중치의 제곱을 더해주는 것이다.
이상치에 대한 W를 0으로 만들지는 않고 0에 가깝게 만든다.
때문에 L1에 비해 L2가 generalization 을 항상 개선시킬 수 있는 것으로 알려져있다.
L2 regulaization을 사용하는 선형 회귀 모델을 Ridge model이라고도 한다.

multiclass SVM loss 외에도 딥러닝에서 자주 쓰이는 softmax가 있다.
multinomial logistic regression이라고도 불린다.
딥러닝에서는 이걸 훨씬 많이 쓴다.
multiclass SVM loss에서는 스코어 자체에 대한 해석은 고려하지 않았다.
스코어 자체는 크게 신경안썼고 safety magin을 포함해서 높은지 낮은지만 판단했다.
하지만 multinomial logistic regression의 손실함수 softmax function은 스코어 자체에 추가적인 의미를 부여한다.
빨간 네모 박스 수식을 이용하여 스코어를 가지고 클래스 별 확률 분포를 계산한다.

in summary 수식을 살펴보면,
(분모) 모든 스코어에 exp를 취하고 그걸 다 더한 다음
(분자) 원하는 클래스의 점수를 exp 취해서 나눈다.
이렇게 되면 '확률' 값이 된다.
예를 들어 1 / 1 + 2 를 하면 1의 확률은 1/3이 된다.
그리고 이걸 -log를 취해서 loss를 계산한다.

그럼 왜 exp와 -log를 붙일까?
softmax는 multinomial logistic regression이다.
logistic regression은 sigmoid function으로도 불린다.
sigmoid function은 위의 그림에서 왼쪽 그래프에 해당된다.
수식을 보면 exp가 취해져있다. 그렇기 때문에 exp를 사용한다.
-log를 취하는 이유는 오른쪽 그림과 같다.
우리는 '얼마나 안좋을지'에 대해 판단해야한다.
x축이 확률, y축이 loss라고 생각하면,
-log가 확률이 1에 가까워질수록 loss가 0에 가까워진다.
즉, x축(확률)에서 우리가 원하는 클래스의 정답률이 1에 가까워질수록 y축(loss)은 0에 가까워진다.
때문에 -log를 사용한다.

직접 계산을 해보자.
아까의 점수에 exp를 취하면 위와 같은 값이 나온다.
그리고 전체를 더한 값 188.68을 각각 나눠준다.
그러면 24.5는 24.5 / 188.68로 0.13이 나오게된다.
마지막으로 원하는 정답 클래스에 -log를 취해준다.
-log(0.13)은 0.89이며, 0.89만큼 안좋다라고 평가할 수 있다.

지금까지 내용을 정리해보자.
우리에세 데이터셋 x와 y가 있다.
입력 x로부터 스코어를 얻기위해 linear classifier를 사용한다.
softmax, svm loss와 같은 손실함수를 이용해서
모델의 예측 값이 정답에 비해 얼마나 별로인지 측정한다.
그리고 모델의 '복잡함'과 '단순함'을 통제하기 위해 손실 함수 regularization term을 추가한다.
지금까지 우리가 supervised learning이라고 부르는 것에 대한 전반적인 개요를 알아보았다.
우리가 딥러닝에서 배울 내용은
어떤 복잡한 함수 f를 정의하고, 그 가중치 값이 주어졌을때
알고리즘이 얼마나 안좋게 동작하는지 측정하는 손실 함수를 작성하는 것이다.
그리고 모델이 복잡해지는것을 어떻게 막을지에 대한 regularization term을 추가한다.
이 모든걸 합쳐서 최종 손실 함수가 최소가 되게 하는 가중치 행렬 W를 구하는 것이다.
그렇다면 실제로 어떻게해야 하는 것일까?
어떻게하면 실제 loss를 줄일 수 있는 w를 찾을 수 있을까?

최적화(optimization)는 우리가 엄청 큰 계곡을 걷고 있는 것과 같다.
다양한 산과 계곡과 시내가 있는 엄청 큰 골짜기를 거닐고 있는 것이다.
그리고 '산'과 '계곡'과 같은 풍경들이 loss라고 보면 된다.
우리가 이 골짜기를 돌아다니는 한 사람이고
있는 곳의 '높이'가 바로 loss이다.
loss는 w에 따라 변하게 되고, 우리는 w를 찾아야 한다.
어떻게든 이 골짜기의 밑바닥을 찾아내야한다.
하지만 일반적으로 이런 문제들은 매우 어렵다.
그렇기 때문에 반복적인 방법 iterative한 방법을 사용한다.
이 방법들은 임의의 지점에서 시작해서 점차적으로 성능을 향상시키는 방법이다.
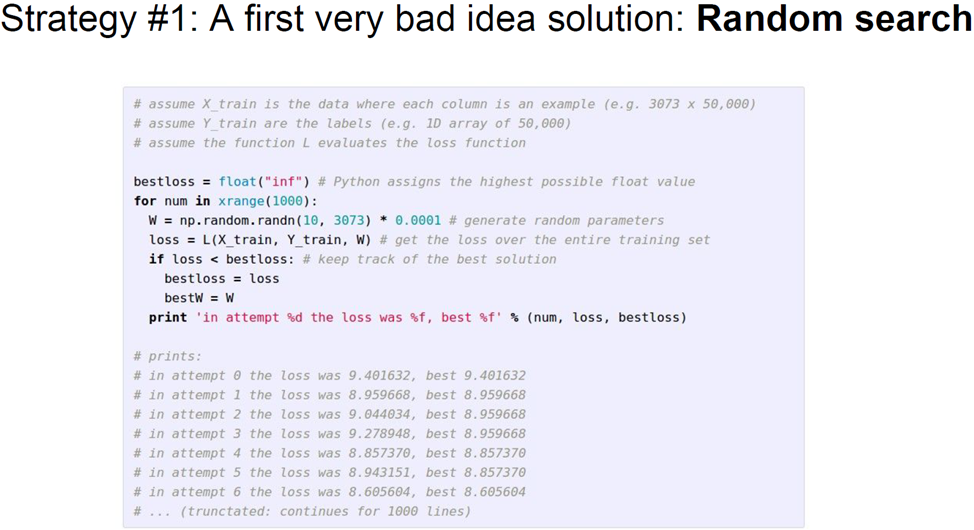
가장 먼저 생각해볼 수 있는 단순한 방법은 임의 탐색(random search)이다.
임의로 샘플링한 W들을 많이 모아놓고 loss를 계산해서 어떤 W가 좋은지 살펴보는 것이다.
이 방법은 절대 사용하면 안된다.
하번쯤은 '상상'해볼만한 방법이긴하다.
위의 그림처럼 실제로 해볼수도 있으며, linear classifier를 학습시킬 수 있다.

cifar-10에서 클래스가 10개이니 임의의 확률은 10%가 되고,
무작위 시행을 거치면 어떤 W를 구해볼 수 있는데 이 예시에서는 약 15% 정확도를 보여준다.
10개중 하나를 찍는 것보다 좀 더 나은 수준이다.
SOTA는 95% 정확도를 가진다 (2017년인걸 감안, 현재는 더 높다)
더 나은 전략은 지역적 기하학 특성(local geometry)을 이용하는 것이다.

위의 그림과 같이 서있다면 어느 방향으로 가야 내려갈 수 있을까?
두 발로 땅의 경사를 느끼고, 어느 방향으로 내려가야할지 느낄 수 있다.
그 방향으로 한발자국 내딛고, 다시 두 발로 느끼는 방향을 다시 찾는다.
이렇게 반복하다보면 결국 골짜기를 다 내려갈 수 있다.

그렇다면 경사(slope)는 무엇일까?
1차원 공간에서 slope는 어떤 함수에 대한 미분값이다.
1차원 함수 f(x) = y 가 있다고 가정하자.
x를 입력으로 받으면 출력은 어떤 커브의 높이라고 할 수 있다.
곡선의 일부를 구하면 기울기를 계산할 수 있다.
어떤 점(x)에서의 경사, 즉 도함수(derivative)를 계산해보면
작은 스텝 h가 있고, 이 스텝 간의 함수 값의 차이를 비교해 보면
f(x+h) - f(x)가 된다.
그리고 이 스텝 사이즈를 0으로 만들면 (h->0)
이것이 바로 어떤 점에서 이 함수의 경사가 된다.
그리고 이 수식을 다변수 함수(multi-variable function)로 확장시킬 수 있다.
실제 x는 스칼라 값이 아닌 벡터 값이 된다.
x가 벡터이기 때문에 위의 개념을 다변수로 확장시켜야 한다.
다변수 상황에서 미분으로 일반화를 해보면 gradient가 되고,
gradient는 벡터 x의 각 요소에 대한 편도함수들의 집합이다.
gradient 모양은 x와 같다. x가 3개면 gradient도 3개.
그리고 gradient의 각 요소가 알려주는 것은 '우리가 그쪽으로 갈때 함수 f의 경사가 어떤지' 이다.
gradient를 이런 유용한 정보를 얻을 수 있다. gradient는 편도함수들의 벡터이다.
gradient의 방향은 함수에서 '가장 많이 올라가는 방향' 이 된다.
반대로는 '가장 많이 내려갈 수 있는 방향'이 된다.
그렇다면 특정 방향에서 얼마나 가파른지 알고 싶으면 어떻게 해야 할까?
해당 방향의 단위 벡터(unit vector)와 gradient 벡터를 내적하면 된다.
gradient는 매우 중요하다. 왜냐하면 gradient가 함수의 어떤 점에서 선형 1차 근사 함수를 알려주기 때문이다.
그래서 실제로 많은 딥러닝 알고리즘들이 gradient를 계산하고,
가중치 W를 반복적으로 업데이트할때 gradient를 사용한다.
컴퓨터로 이 gradient를 써먹을 수 있는 가장 단순한 방법 중 하나는,
유한 차분법(finite difference method)를 이용하는 것이다.

왼쪽에 가중치(파라미터) 벡터 W가 있다.
이 W를 사용하면 1.25347 loss를 가진다.
여기서 우리는 gradient 'dW'를 구해야 한다.
gradient의 각 요소가 말해주는 것은 우리가 한 방향으로 아주 조금 이동했을때
loss가 어떻게 변하는지에 대한 것이다.
일단 W가 있고, W의 첫번째 요소 0.34에 아주 작은 값 h, 0.0001을 더해보는 것이다.
그리고 다시 loss를 계산한다.
loss가 1.25322로 기존의 1.25347보다 loss가 줄은 것을 볼 수 있다.
이는 첫 번째 요소를 조금 움직이면 loss가 감소한다는 사실을 알 수 있다.
이제 극한 식을 이용해서 유한 차분법으로 근사시킨 gradient를 구한다.
첫번째 요소의 gradient는 -2.5이다.
이제 첫 번째 요소의 값은 원래대로 돌려놓고
두번째 요소를 h 만큼 증가시킨다.
그리고 다시 loss를 계산하고 유한 차분법을 이용해서
두번째 요소의 gradient의 근사치를 계산할 수 있다.
이렇게 계속 반복합니다.


이는 시간이 엄청 오래걸리는 방법이다.
이 함수 f가 CNN과 같이 엄청 큰 함수였다면, 훨씬 더 오래 걸릴 것이다.
여기서는 파라미터 W가 10개뿐이 없지만
크고 깊은 신경망에서는 파라미터가 수천, 수억개일 수 있다.
그렇기 때문에 실제로는 이런식으로 gradient를 계산하지 않는다.
왜냐하면 gradient 하나를 계산하기 위해 수천개의 함수값을 일일이 다 계산해야하기 때문이다.

위의 두 인물(아이작 뉴턴, 라이프니츠) 덕분에 손실 함수를 적어놓고 '미분'이라는 마법의 망치를 두드리면
gradient가 계산되서 나온다.
해석적(analytic)으로 계산하는 것이 수치적으로 계산하는 것보다 더 효율적이다.
더 정확하기도 할 뿐더러, 식 하나로 계산할 수 있기 때문에 훨씬 더 빠르다.

W의 모든 원소를 순회하면서 gradient를 계산하는것이 아니라,
gradient를 나타내는 식이 무엇인지 찾고
그걸 수식으로 나타내서 한번에 gradient dW를 계산하는 것이다.

위의 세 줄의 간단한 알고리즘은
크고 복잡한 신경망 알고리즘을 어떻게 학습시킬것인가에 대한
핵심 아이디어를 지니고 있다.
gradient descent는 우선 w를 임의의 값으로 초기화한다.
그리고 loss와 gradient를 계산하고,
가중치를 gradient 반대 방향으로 업데이트한다.
gradient가 함수에서 증가하는 방향이기 때문에
-gradient를 해야 반대방향으로 내려가는 방향이 된다.
그럼 -gradient 방향으로 조금씩 이동할 것이고
이걸 계속 반복하다보면 결국 수렴할 것이다.
하지만 스텝 사이즈는 하이퍼파라미터이다.
스텝 사이즈는 -gradient 방향으로 얼마나 나아가야하는지 알려준다.
스텝 사이즈를 학습률(learning rate)이라고도 하며,
실제 학습시 정해줘야하는 가장 중요한 하이퍼파라미터중 하나이다.

위의 그림은 2차원 공간에서의 gradient descent 예시이다.
하얀색 원이 손실함수이다.
가운데 빨간 부분이 낮은 loss이고 파란색으로 갈수록 높은 loss를 나타낸다.
임의의 점 W를 설정하고 -gradient를 계산해서
loss가 낮은 지점에 도달할 것이다.
이걸 계속 반복하게 되면 결국은 최저점에 도달할 수 있을 것이다.

손실 함수 정의를 생각해보면
loss는 각 트레이닝 샘플을 분류기가 얼마나 '안좋게' 분류하는지를 계산하는것이고,
전체 loss는 전체 트레이닝셋 loss합의 평균을 사용했다.
하지만 실제로는 N(트레이닝 샘플)이 엄청 커질 수 있다.
ImageNet 데이터셋의 경우 N은 130만개이다.
따라서 loss를 계산하는것은 매울 오래걸리는 작업이 된다.
수백만번의 계산이 필요할 수 있으며, 이는 매우 느릴 수 있다.
gradient는 선형 연산자이기 때문에
실제 gradient를 계산하는 과정을 보면,
loss는 각 데이터 loss의 gradient 합계라는 것을 알 수 있다.
그렇기 때문에 gradient를 한번 더 계산하려면,
N개의 전체 데이터셋을 한번 더 돌면서 계산해야한다.
N이 130만이면 엄청 느릴수밖에 없다.
W가 업데이트 되려면 엄청 많은 시간을 기다려야할 것이다.
그래서 실제로는 stochastic gradient descent 방법을 쓴다.
전제 데이터셋의 gradient와 loss를 계산하는것이 아니라
mini-batch라는 작은 트레이닝 샘플 집합으로 나눠 학습을 진행한다.
mini-batch는 보통 2의 승수로 정하며, 보통 32, 64, 128을 사용한다.
작은 mini-batch를 이용해서
loss의 전체 합의 '추정치'와
실제 gradient의 '추정치'를 계산한다.
그래서 stochastic 하다는 것은 Monte Carlo Method의 실제 값 추정 방법과 유사하다고 볼 수 있다.
코드가 4줄로 늘었다.
임의의 mini-batch를 만들어내고 mini-batch에서 loss와 gradient를 계산한다.
그리고 W를 업데이트한다.
loss의 '추정치'와 gradient의 '추정치'를 사용하는 것이다.
SGD는 거의 모든 Deep NN알고리즘에 사용되는 기본적인 학습 알고리즘이다.
이제 이미지 특징(feature)에 대해 살펴보자.

linear classifier는 실제 raw image 픽셀을 입력으로 했다.
하지만 이런 방법은 좋은 방법이 아니다.
multimodality와 같은 이유 때문이다. (말 머리 두개)
영상 자체를 입력으로 사용하는 것은 성능이 좋지 않다. (hand crafted feature 관점에서)
그래서 DNN이 유행하기 전에 주로 쓰는 방법은 2 stage를 거치는 것이였다.
첫번째는 이미지가 있으면 여러가지 특징 표현을 계산하는 것이다.
이런 특징 표현은 이미지의 모양새와 관련된 것일 수 있다.
그리고 여러 특징 표현들을 연결(concat)시켜 하나의 특징 벡터로 만든다.
이러한 특징 벡터가 linear classifier의 입력으로 들어가는 것이다.

위의 그림과 같이 트레이닝셋이 있다고 가정하자.
빨간점들이 가운데 있고 주변에 파란점들이 있다.
이 데이터셋에서 linear한 결정 경계를 그릴 방법이 없다.
하지만 적절한 특징 변환을 거친다면,
복잡한 데이터가 변환 후 선형으로 분리 가능하게 바뀔 수 있다.
이런 방법은 문제를 풀 수 있도록 하려면 어떤 특징 변환이 필요한가를 알아내는 것들이다.
이미지의 경우 픽셀을 극좌표계로 바꾸는것이 말이 안되지만
극좌표계로 바꾸는것을 일종의 특징 변환이라고 생각한다면 이해될 수 있다.
실제로 분류기에 raw 픽셀값을 넣는것보다 성능이 더 좋을수도 있다.

특징 변환의 예로 컬러 히스토그램이 있다.
이미지의 hue 값만 뽑아서 모든 픽셀을 카운팅하는것이다.
해당하는 색상의 픽셀 개수를 세는 것이다.
이는 이미지가 전체적으로 어떤 색인지 알려준다.
위의 개구리를 보면 초록색 계열이 많은 것을 볼 수 있다. 자주색이나 붉은색은 별로 없다.
실제로 사용하는 간단한 특징 벡터라고 볼 수 있다.

NN이 뜨기 전에 인기있었던 특징 벡터 중 하나는 histogram of oriented gradients(HOG)이다.
local orientation edges를 측정한다.
이미지를 8x8 픽셀로 나누고, 이 지역 내에서 가장 영향력있는 edge의 방향을 계산한다.
그리고 이를 양자화해서 histogram을 만든다.
다양한 edge orientation에 대한 히스토그램을 계산하는 것이다.
그러면 전체 특징 벡터는
각각의 모든 8x8 지역들이 가진 edge orientation에 대한 히스토그램이 되는 것이다.
위의 개구리를 보면 이파리 위에 앉아있는 것을 볼 수 있다.
이파리들은 주로 대각선 edge를 가지고 있다.
HoG로 시각화해 보면 이파리 부분에 많은 대각 edge가 있다는 것을 알 수 있다.
이는 HoG의 특징 표현이라고 볼 수 있다.
HoG는 영상 인식에서 정말 많이 활용한 특징 벡터이다.

또 하나의 특징 표현은 Bag of Words(BOW)이다.
이 아이디어는 자연어처리(NLP)에서 영감을 받은 것이다.
어떤 문장이 있고 BOW에서 이 문장을 표현하는 방법은
문장의 여러 단어의 발생 빈도를 세서 특징 벡터로 사용하는 것이였다.
이와 같은 직관을 이미지에 적용한 것이 BOW이다.
우선 시각 단어(visual words)라고 하는 용어를 정의했으며,
2단계의 과정을 거친다.
엄청 많은 이미지를 이용해서 그 이미지들을 임의로 조각낸다.
그리고 그 조각들을 k-means와 같은 알고리즘으로 군집화한다.
이미지내의 다양한 것들을 표현할 수 있는 다양한 군집들을 만들어내는 것이다.
위의 그림에서 오른쪽을 보면, (step 1)
이는 이미지들에서 다양한 이미지 패치를 뽑아서 군집화 시켜 높은 예이다.
군집화 단계를 거치면 시각 단어는 빨간색, 노란색, 파랑색과 같은 다양한 색을 포착할 수 있다.
또한 다양한 방향의 oriented edge들도 포착할 수 있다.
이 방법은 edge들을 데이터 중심적인 방법을 통해 얻어냈다는 점에서 매우 흥미롭다.
이런 시각 단어 집합인 'codebook'을 만든 다음,
어떤 이미지가 있으면 이 이미지에서 시각 단어들의 발생 빈도를 통해
이미지를 인코딩 할 수 있다.
이는 이 이미지가 어떻게 생겼는지에 대한 다양한 정보를 제공한다.

Image classification의 pipe line은 위의 그림과 같다.
5~10년 전까지만 해도 이미지를 입력받으면
BOW나 HOG와 같은 다양한 특징 표현을 계산하고,
계산된 특징들을 모아 연결해서 만든 벡터를 linear classifier의 입력으로 사용했다.
특징이 한번 추출되면 feature extractor는 분류기를 학습하는동안 업데이트하지 않는다.
학습중에는 오직 linear classifier만 학습이 된다.
DNN을 보면 크게 다르진 않지만
이미 만들어 놓은 특징들을 사용하는것이 아닌
데이터로부터 특징들을 직접 학습하려한다는 점이 다른점이다.
그렇기 때문에 raw 픽셀이 cnn에 그대로 입력되고
여러 레이어를 거쳐서 데이터를 통한 특징 표현을 직접 만들어내게 된다.
따라서 linear classifier만 훈련하는게 아니라
가중치 W 전체를 한번에 학습한다.
'머신러닝 > CS231n (2017)' 카테고리의 다른 글
| Lecture 5: Convolutional Neural Networks (0) | 2020.09.24 |
|---|---|
| Lecture 4: Backpropagation and Neural Networks (0) | 2020.09.17 |
| Lecture 2: Image Classification Pipeline (0) | 2020.09.12 |
| Lecture 1: Introduction (0) | 2020.09.07 |
| 시작하기 앞서 (0) | 2020.09.07 |