조마조마

part 1에서는 활성 함수, 데이터 전처리, 가중치 초기화, batch normalization, 학습 과정, 하이퍼파라미터 최적화를 다룬다.

 

먼저 activation functions을 살펴보자.

 

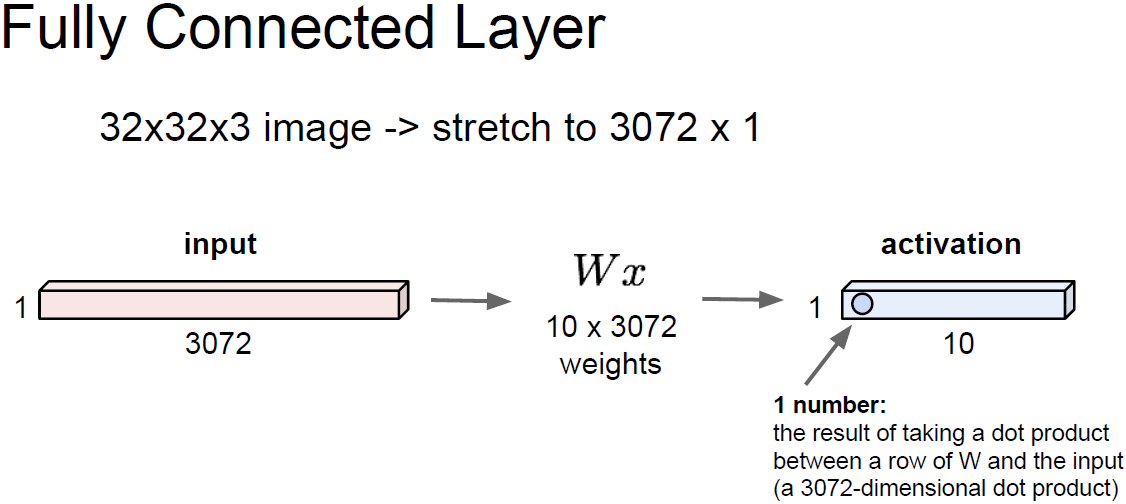
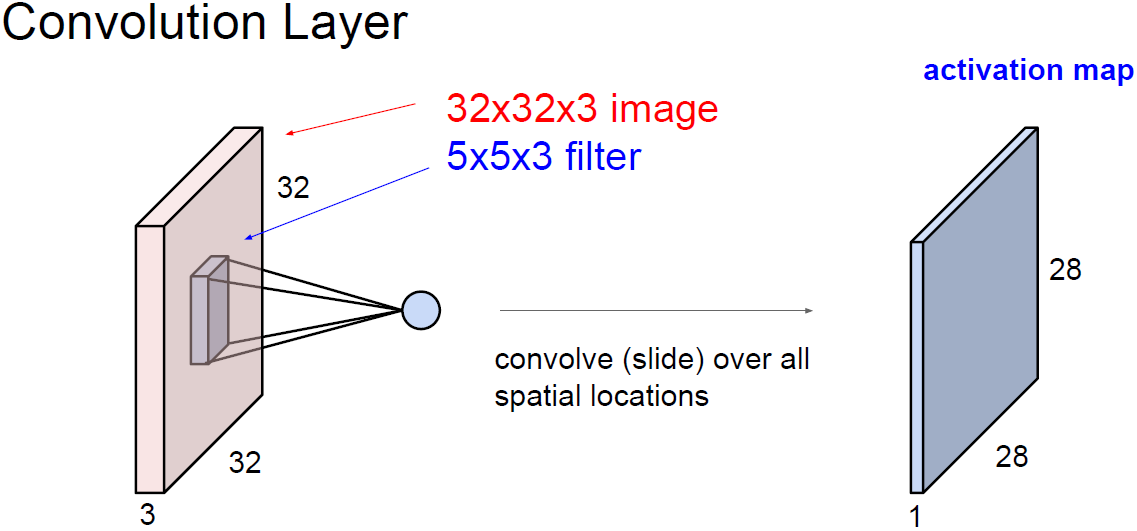
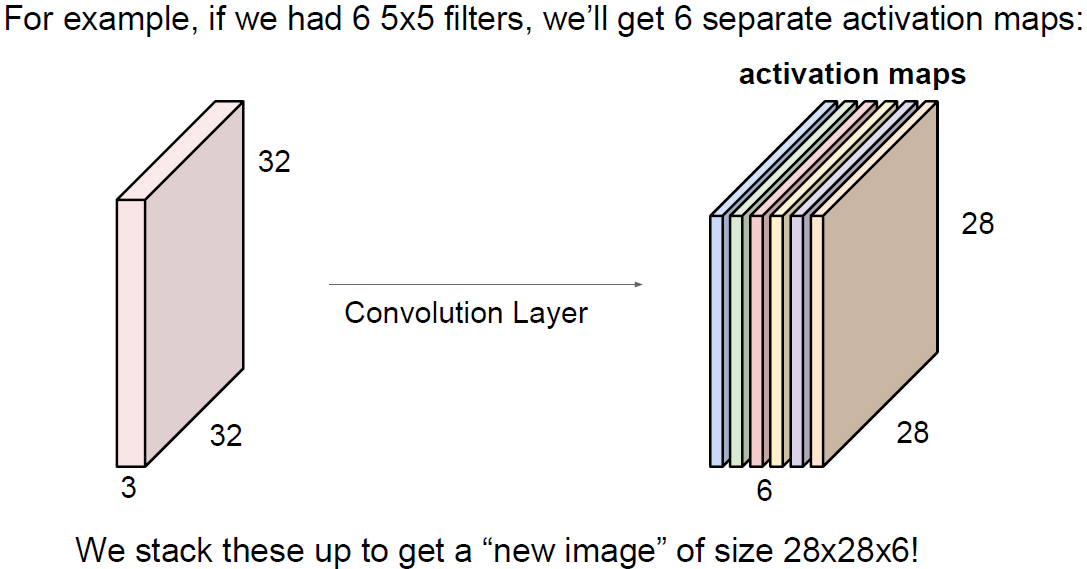
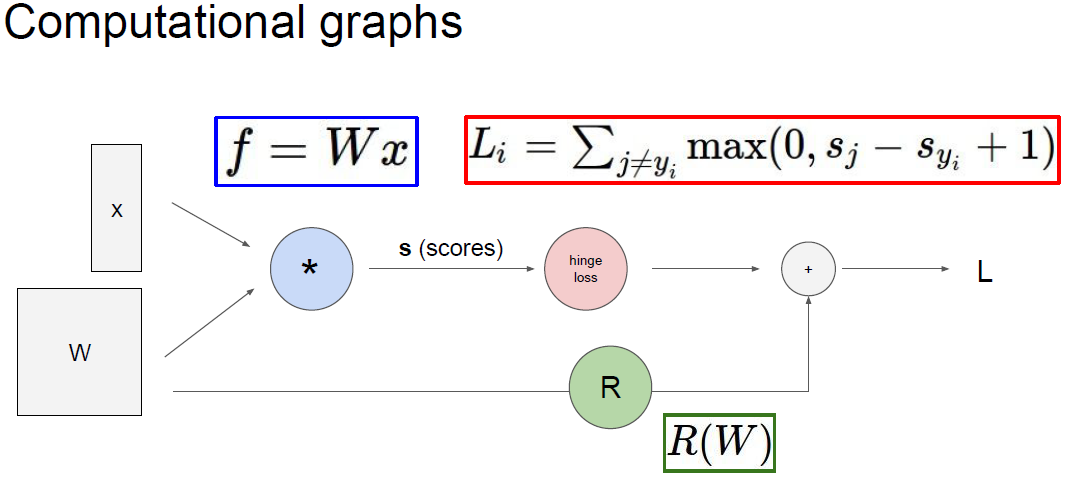
input으로 데이터 입력이 들어오고 가중치와 곱한다. (행렬 내적)

 

이는 FC 혹은 CNN이 될 수 있다.

 

이후 활성 함수(activation function), 즉 비선형 함수를 통과하게 된다.

 

위의 그림은 다양한 활성 함수들의 예시를 보여준다.

 

먼저 sigmoid를 살펴보자.

 

sigmoid는 입력을 받아서 0~1 사이의 값이 되도록 한다.

 

입력이 크면 1에 가깝고, 입력이 작으면 0에 가깝게 된다.

 

0 근처의 구간을 보면 선형 함수와 가까워 보인다.

 

이는 값이 적당할때 back-propagation이 잘될거라고 알 수 있다.

 

sigmoid는 역사적으로 유명하다.

 

왜냐하면 neuron을 firing rate를 saturation 시키는 것으로 해석할 수 있기 때문이다.

 

어떤 값이 0에서 1사이의 값을 가지고 있으면,

 

이를 firing rate로 생각할 수 있다.

 

생물학적으로는 0 보다 큰 값을 그대로 활성화 시키는 relu가 더 타당성이 크다는게 밝혀졌지만,

 

sigmoid 또한 firing rate를 saturation 시킨다는 관점에서 해석할 수 있다.

 

하지만 몇가지 문제점이 있다.

 

첫번째는 saturation 되는 것이 gradient를 없애는 것이다.

 

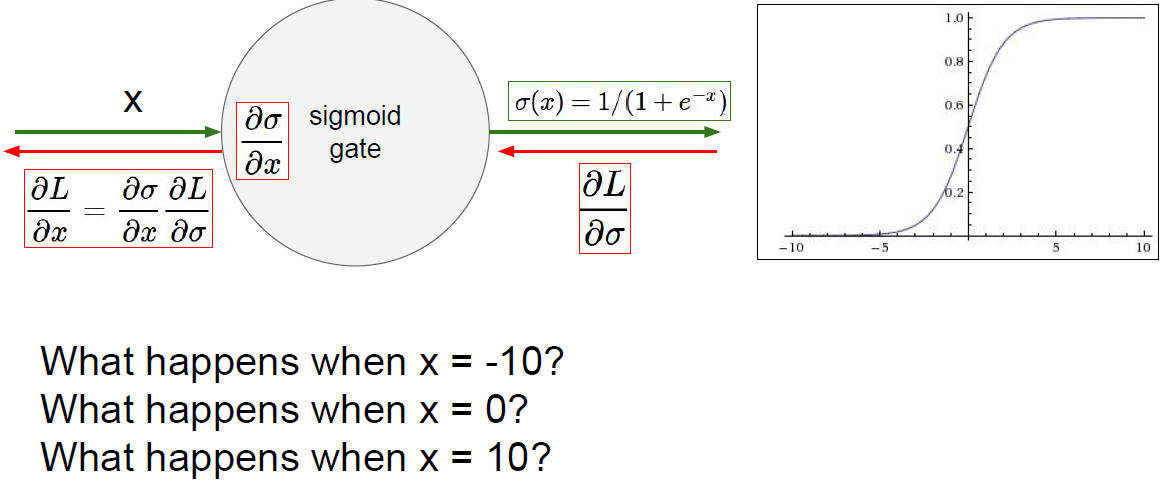
입력 x에 -10을 대입하고 sigmoid function을 통과하면 backprop에서 gradient는 어떻게 될까?

 

우선 dL / dSigma와 dSigma/dx의 곱이 sigmoid function의 gradient가 된다. (chain rule)

 

이렇게 계산된 gradient는 계속 아래로 흐르며 backprop 될 것이다.

 

그럼 입력 x가 -10일 때 gradient는?

 

0에 한없이 가깝게 된다.

 

sigmoid에서 음의 큰 값은 sigmoid가 평평하게 되고 gradient는 0에 가깝게 된다.

 

이렇게되면 0에 가까운 값이 계속 아래로 흐르며 backprop 될 것이다.

 

입력 x가 0이 면 어떻게 될까?

 

이 구간은 backprop가 잘 동작될 것이다.

 

그럴싸한 gradient를 얻을 수 있다는 말이다.

 

그럼 입력 x가 10이면 어떻게 될까?

 

x값이 양의 큰 값일 경우에도 sigmoid가 평평하게 되고 gradient가 0에 가깝게 된다.

 

두번째 문제는 sigmoid 출력이 zero centered 하지 않는 점이다.

 

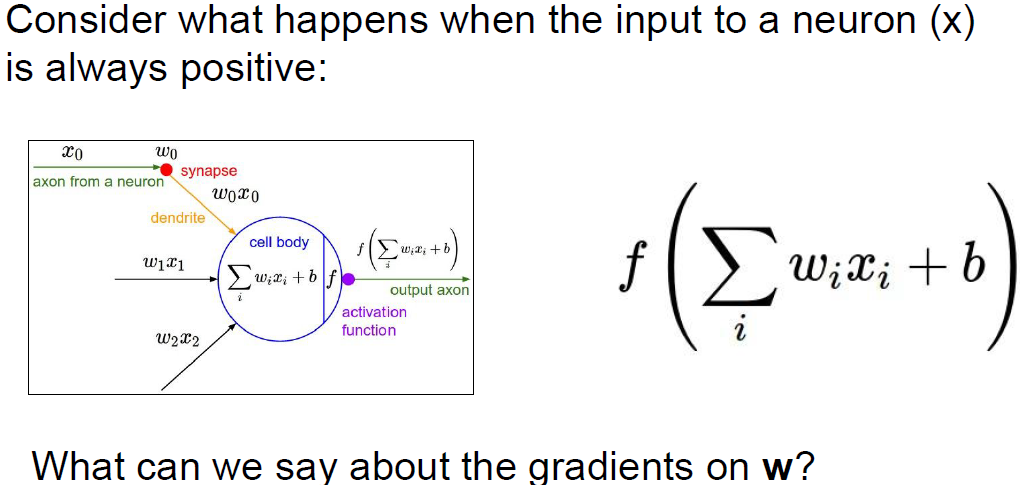
neuron의 입력이 항상 양수일때 어떻게 될까?

 

입력 양수 x는 가중치와 곱해지고 활성함수를 통과할 것이다.

 

이때 가중치 w에 대한 gradient를 생각해보자.

 

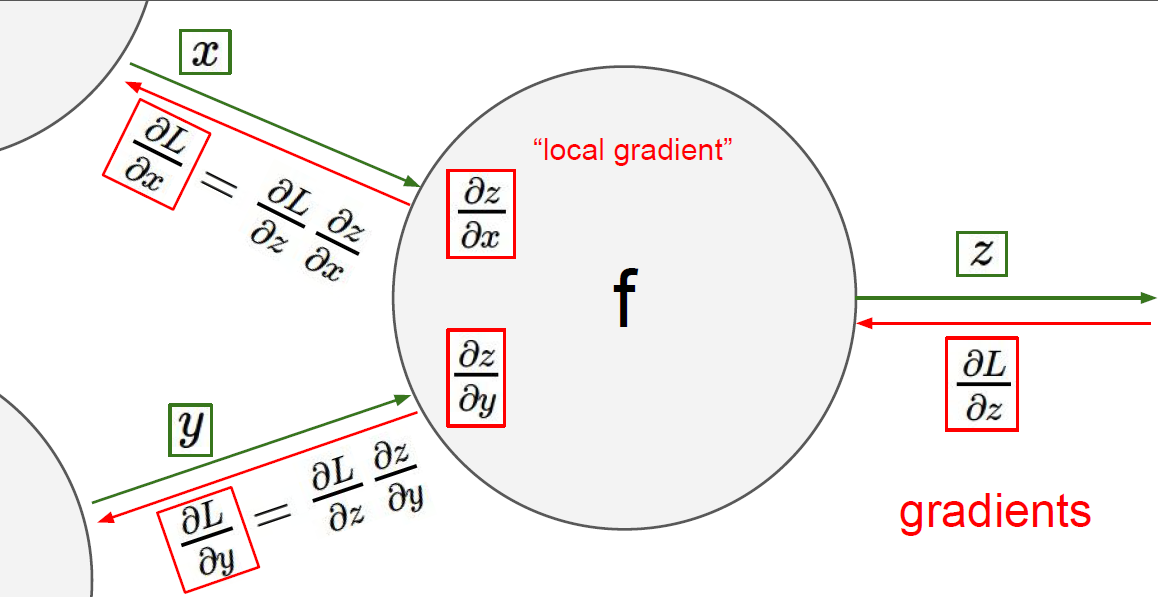
우선 dL/df(activation function)를 계산해서 loss가 아래로 흐를 것이다.

 

그리고 아래에서 (기본적으로 x라고 하자) local gradient가 있을텐데,

 

모든 x가 양수라면 해당 gradient는 '전부 양수' 혹은 '전부 음수'가 된다.

 

위에서 흘러온 dL/df(activation function)의 값이 양수 또는 음수가 될 것이다.

 

어떤 임의의 gradient가 흘러왔다고 가정하면,

 

우선 local gradient는 흘러온 값과 곱해질 것이고

 

df(activation function)/dw는 단지 x가 된다.

 

그렇게되면 gradient의 부호는 위에서 흘러온 gradient의 부호와 같아지게 된다.

 

이는 가중치 w가 모두 같은 방향으로만 움직일것이라는 것을 의미한다.

 

파라미터가 업데이트될 때 전부 증가하거나 전부 감소하게 된다.

 

이러한 gradient update는 굉장히 비효율적이다.

 

위의 그림 오른쪽은 w의 이차원 예제이다.

 

w에 대한 두개의 축이 있다.

 

전부 양수 혹은 음수로 update된다면 gradient가 이동할 수 있는 방향은

 

4분면 중 2개의 영역뿐이 되질 않는다.

 

2분면과 3분면의 방향으로만 업데이트 된다.

 

위의 오른쪽 그림에서 가장 최적의 w 업데이트가 파란색 화살표라고 가정하면,

 

초기 시작점(첫 빨간색 화살표)부터 업데이트한다고 했을 때,

 

파란색 방향으로 잘 내려갈 수 없게 된다.

 

때문에 여러번의 업데이트를 수행하게 된다. (빨간 화살표)

 

이것이 zero-mean data가 필요한 이유가 된다.

 

입력 x가 양수와 음수 모두 가지고 있다면,

 

전부 같은 방향으로 업데이트되는 일이 발생하지 않을 것이다.

 

세 번째 문제는 exponential 함수로 인해 계산 비용이 크다는 점이다.

 

하지만 이 문제는 그리 큰 문제가 아니다.

 

비용 측면에서 보면 내적과 같은 연산의 비용이 더 크다.

 

굳이 문제를 뽑자면 exp() 비용을 꼽는다는 것이다.

 

두 번째 활성 함수는 tanh이다.

 

sigmoid와 유사하지만 범위가 -1~1 사이의 값을 가진다.

 

가장 큰 차이점이라면 zero-centered라는 것이다.

 

이를 통해 sigmoid의 두 번째 문제가 해결된다.

 

하지만 saturation되기 때문에 여전히 낮거나 높은 값에서의 gradient가 0에 가깝게 되버린다.

 

tanh는 sigmoid보다는 조금 낫지만 그래도 위처럼 여전히 문제점이 있다.

 

이제 ReLU를 살펴보자.

 

이전에 봤던 CNN 모델들을 보면 conv layer 사이 사이에 ReLU가 있는 것을 볼 수 있었다.

 

ReLU 함수는 f(x) = max(0,x) 이다.

 

이 함수는 element-wise 연산을 수행하면서 

 

입력이 0 미만의 음수면 출력이 0이 된다.

 

그리고 입력값이 양수면 출력은 입력값 그대로를 출력한다.

 

기존 sigmoid와 tanh에게 있었던 문제점들을 ReLU에서 살펴보면,

 

우선 양수 값에서는 saturation되지 않는 것을 알 수 있다.

 

이는 적어도 입력 공간의 절반은 saturation되지 않을 것이며 ReLU의 가장 큰 장점이다.

 

그리고 계산 효율이 뛰어나다.

 

sigmoid는 계산 수식에 지수 항이 있었다.

 

반면 ReLU는 단순 max 연산이기 때문에 계산이 상대적으로 빠르다.

 

ReLU를 사용하면 실제로 sigmoid와 tanh 보다 수렴속도가 거의 6배 정도로 빠르다.

 

그리고 위에 언급했지만 생물학적 관점에서도 ReLU가 sigmoid보다 좀 더 알맞다.

 

실제 신경과학적 실험을 통해 neuron을 관찰해보면

 

sigmoid 보다는 ReLU스럽다는 것이다.

 

2012년 ImageNet에서 우승한 AlexNet에서 처음 ReLU를 사용하기 시작했다.

 

하지만 zero-centered한 문제를 해결하지는 못했다.

 

또한 양수에서는 saturation되지 않지만 음수에서는 그렇지 못하다.

 

입력 x가 -10일 경우 어떻게 될까?

 

gradient는 0이 된다.

 

입력 x가 10일 경우는 linear한 영역에 속하기 때문에 그럴싸한 gradient가 계산될 것이다.

 

x가 0일때의 gradient는 0이 된다.

 

기본적으로 ReLU는 gradient의 절반을 죽이는 것이다.

 

그래서 dead ReLU라는 현상을 겪을 수 있다.

 

위의 그림은 training data를 2차원 초평면 공간에 나타낸 그림이다.

 

여기서 ReLU는 평면의 절반만 activatite 하는 것을 알 수 있다.

 

ReLU가 training data에서 떨어져 있는 경우 dead ReLU가 발생할 수 있다.

 

dead ReLU에서는 activate가 일어나지 않으며 업데이트 되지 않는다.

 

반면에 activate ReLU에서는 일부 activate되고 일부 activate하지 않을 것이다.

 

몇 가지 이유로 이런 일이 발생할 수 있다.

 

첫 번째는 초기화가 잘못됐을 경우이다.

 

가중치 평면아 training data에서 멀리 떨어져 있는 경우이다.

 

이런 경우 어떠한 입력에서도 활성화되지 않을 것이고 backprop이 일어나지 않을 것이다.

 

업데이트도 활성화도 되지 않는다.

 

또 하나의 경우는 learning rate가 지나치게 높은 경우이다.

 

처음에는 적절한 초기화 인해 적절한 ReLU로 시작할 수 있다고 해도

 

업데이트를 지나치게 크게 해서 가중치가 널뛴다면

 

ReLU는 데이터의 manifold를 벗어나게 된다. (ReLU가 데이터의 차원을 벗어났다고 생각하면 될듯)

 

위의 일들은 학습 과정에서 충분하게 일어날 수 있다.

 

그래서 처음에는 학습이 잘 되다가 갑자기 안되는 경우가 생기는 것이다.

 

그리고 실제로 학습이 된 네트워크를 살펴보면

 

10~20% 가량은 dead ReLU가 되어 있다.

 

ReLU를 사용하면 대부분의 네트워크가 이 문제를 겪을 수 있다.

 

하지만 이 정도는 네트워크 학습에 크게 지장이 없다고 한다.

 

그래서 실제로 ReLU를 초기화할 때 positive biases(0.01정도)를 추가해 주는 경우가 있다.

 

가중치 업데이트 시 activate ReLU가 될 가능성을 조금이라도 더 높혀주기 위함이다.

 

하지만 이 positive biases가 도움이 된다는 의견도 있고 그렇지 않다는 의견도 있다.

 

보통은 zero-bias로 초기화한다.

 

ReLU 이후에 살짝 수정된 Leaky ReLU가 나왔다.

 

ReLU와 유사하지만 negative 영역이 더 이상 0이 아니다.

 

negative에도 기울기를 살짝 주게되면 앞의 문제를 상당 부분 해결할 수 있다.

 

leaky ReLU의 경우 음수의 경우에도 saturation되지 않는다.

 

여전히 sigmoid와 tanh 보다 수렴을 빨리 할 수 있다.

 

또한 dead ReLU 현상도 사라진다.

 

또 다른 예시로 parametric rectifier, PReLU가 있다.

 

PReLU는 negative 영역에 기울기가 있다는 점에서 leaky ReLU와 유사하지만

 

기울기를 가중치 a(알파) 파라미터로 결정된다.

 

가중치 a는 정해진것이 아니며 backprop을 통해 학습이 된다.

 

activation function이 좀 더 유연해 질 수 있다.

 

ELU라는 것도 있다.

 

ELU는 ReLU의 이점을 그대로 가져온다.

 

하지만 ELU는 zero-mean에 가까운 출력값을 보인다.

 

zero-men에 가까운 출력은 leaky ReLU 및 PReLU가 가진 장점이였다.

 

하지만 leaky ReLU와 비교해보면 ELU는 negative영역에서 saturation된다.

 

ELU는 이런 saturation이 noise에 강인할 수 있다고 한다.

 

이런 deactivation이 좀 더 강인함을 줄 수 있다고 논문에서 주장한다.

 

ELU는 ReLU와 leaky ReLU의 중간정도라고 보면 된다.

 

ELU는 leaky ReLU처럼 zero-mean의 출력을 갖지만 

 

saturation 관점에서 ReLU의 특성 또한 지니고 있다. (negative 영역)

 

Maxout이라는 활성화 함수도 있다.

 

무려 Generative Adversarial Network(GAN)의 창시자 이안굿펠로우가 2013년에 논문을 낸 내용이다.

 

dot product의 기본적인 form을 미리 정의하지 않는다.

 

대신 w1에 x를 내적한 값 + b1과 w2에 x를 내적한 값 + b2의 최대값을 사용한다.

 

maxout은 이 두 함수 중 최대값을 취한다.

 

maxout은 ReLU와 leaky ReLU의 좀 더 일반화된 형태이다.

 

왜냐하면 maxout은 위 두 개의 선형함수 중 최대값을 취하므로

 

선형이기 때문에 saturation되지 않으며 gradient를 잘 계산할 것이다.

 

하지만 문제점은 파라미터의 수가 두배가 된다는 점이다. (w1, w2)

 

가장 많이 쓰이는 활성 함수는 ReLU이다.

 

ReLU가 표준으로 많이 쓰이며 대부분 잘 동작한다.

 

하지만 위에도 언급했듯이 ReLU 사용 시 learning rate를 잘 설정해야 한다.

 

실제 네트워크를 학습하려면

 

일반적으로 입력 데이터에 대한 전처리가 필요하다.

 

가장 대표적인 전처리 과정은 zero-mean으로 만들고 normalize 해주는 것이다.

 

normalization은 보통 표준편차 이용해서 수행한다.

 

그럼 이러한 전처리가 왜 필요한것일까?

 

앞에서 입력이 전부 positive인 경우인 zero-centered에 대해 언급했다.

 

그렇게되면 모든 neuron이 positive gradient를 얻게 되고

 

이는 최적화가 아닌 최적화가 되버린다.

 

입력 데이터가 전무 positive 뿐만 아니라 전부 0 이거나 전부 negative인 경우에도 동일하다.

 

normalization을 해주는 이유는 모든 차원이 동일한 범위를 갖게 함으로써

 

전부 동등한 contribute를 할 수 있게 한다.

 

입력 데이터가 이미지일 경우 전처리로 zero-centering 정도만 해준다.

 

normalization은 하지 않는다.

 

왜냐하면 이미지는 이미 각 차원 간에 스케일이 어느정도 맞춰져있기 때문이다.

 

따라서 스케일이 다양한 여러 machine learning 문제와는 달리

 

이미지에서는 normalization을 엄청 잘 해줄 필요가 없다.

 

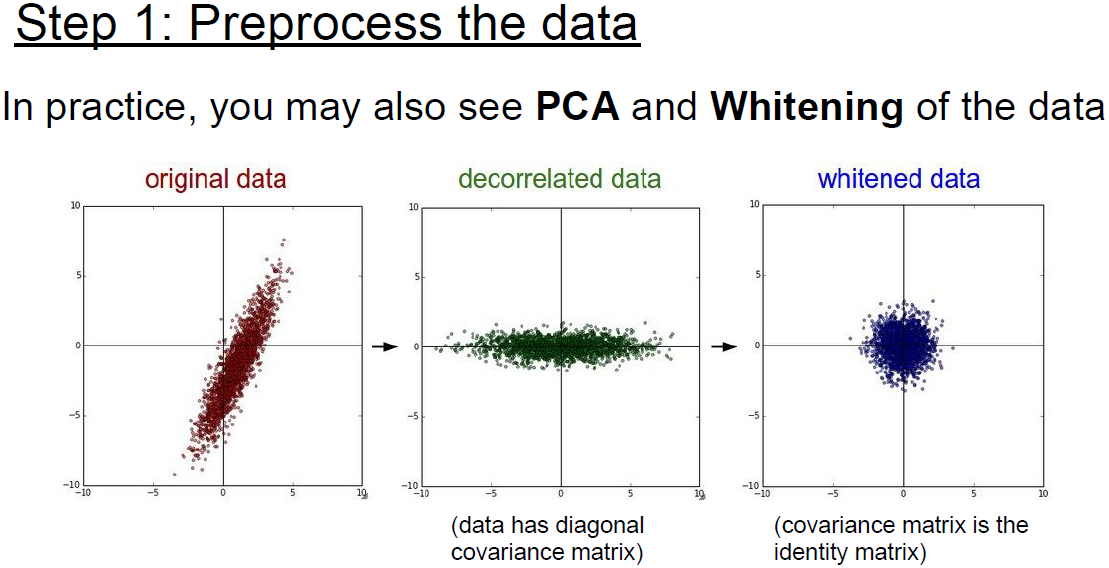
ml에서는 PCA 혹은 whitening과 같은 복잡한 전처리 과정도 있지만

 

이미지에서는 단순히 zero-mean 정도만 사용하고

 

normalization을 비롯한 여러 복잡한 방법들은 잘 쓰이지 않는다.

 

일반적으로 이미지를 다룰 때는 굳이 입력을 더 낮은 차원으로 projection 시키지 않는다.

 

CNN에서는 원본 이미지 자체의 spatial한 정보를 활용해서 이미지의 spatial 구조를 얻을 수 있도록 한다.

 

이미지에서의 zero-mean은

 

training data에서 평균 값을 계산하고 이 평균값을 네트워크에 입력되기 전에 빼준다.

 

inference할때도 training data 평균값을 빼주게 된다. (ex. AlexNet)

 

일부 네트워크는 이미지 컬러 채널 전체의 평균을 구하지 않고

 

채널마다 평균을 독립적으로 계산하는 경우도 있다. (ex. VGGNet)

 

이제 weight를 어떻게 초기화 시켜야 하는지에 대해 살펴보자.

 

위의 그림 two layer neural network를 예시로 보자.

 

우리가 할 일은 가중치 업데이트이다.

 

어떤 초기 가중치들이 있고 gradient를 계산해서 가중치를 업데이트할 것이다.

 

이때 모든 가중치를 0으로 하면 어떻게 될까?

 

그렇게된다면 모든 가중치가 동일한 연산을 수행하게 된다.

 

출력도 모두 같게 되며, 결국 gradient도 서로 동일하게 된다.

 

이는 모든 가중치가 똑같은 값으로 업데이트 된다.

 

모든 neuron이 동일하게 생기게 된다.

 

이는 모든 가중치를 동일하게 초기화시키면 발생하는 일이다.

 

이런 초기화 문제를 해결하는 첫번째 방법은

 

임의의 작은 값으로 초기화하는 것이다.

 

이 경우 초기 w를 standard gaussian(표준정규분포)에서 샘플링한다.

 

작은 네트워크라면 이런식의 초기화로 충분하지만

 

깊은 네트워크에서는 문제가 발생할 수 있다.

 

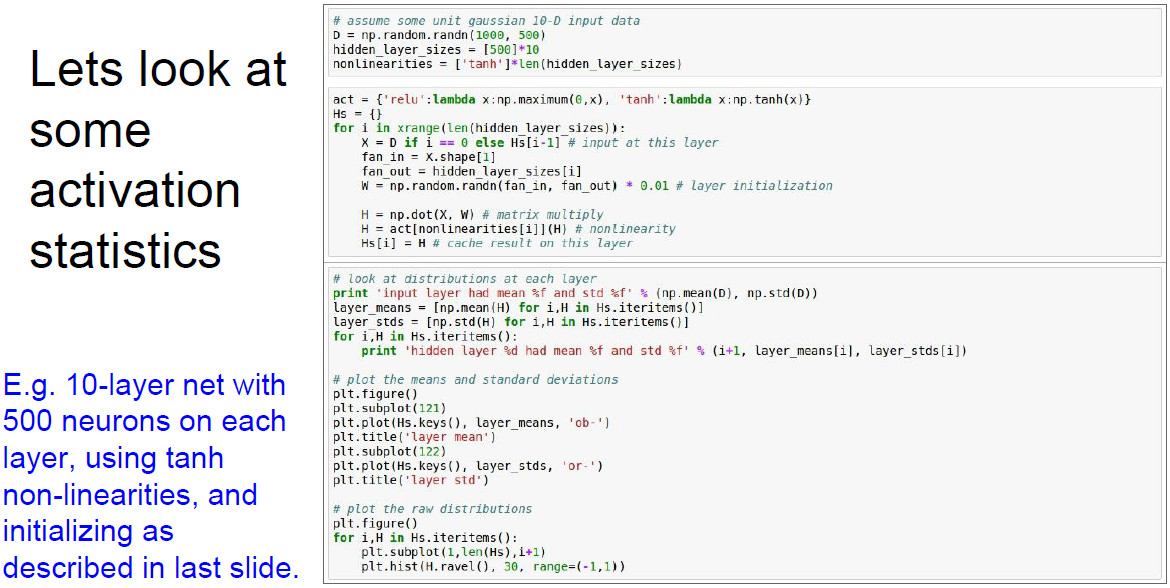
10개 layer로 이루어진 네트워크가 있다.

 

layer당 500개의 neuron이 있다.

 

활성 함수로는 tanh를 사용한다.

 

그리고 가중치는 임의의 작은 값으로 초기화시킨다.

 

데이터를 임의의 값으로 생성하고 forward pass를 시킨다.

 

그리고 각 레이어별 activation 수치를 통계화시키면 아래 그림과 같다.

 

위 수치는 각 layer 출력의 평균과 평균의 표준편차를 계산한 것이다.

 

중간의 왼쪽 그래프가 layer마다의 mean을 나타낸다.

 

평균은 항상 0 근처에 있다. (tanh 특성, zero-centered)

 

중간의 오른쪽 그래프가 layer마다의 std를 나타낸다.

 

이 std 보면 가파르게 줄어들면서 0에 수렴한다.

 

아래 그림은 layer별 std를 분포로 표현한 것이다.

 

첫번째 layer는 gaussian처럼 생긴 좋은 분포를 형성하고 있다.

 

문제는 w를 곱하면 곱할수록 값이 작아져서 출력 값이 급격히 줄어든다는 점이다.

 

backwards pass로 다시한번 살펴보자.

 

각 layer의 입력이 매우 작은 값이다. 이 값들은 점점 0에 수렴한다.

 

backprop를 생각해보면 upstream gradient가 점점 전파된다.

 

현재 가중치를 업데이트하려면 upstream gradient에 local gradient를 곱해주면 된다. (chain rule)

 

우선 wx를 w에 대해 미분하면 local gadient는 입력 x가 된다. (w의 gradient는 x)

 

x가 매우 작은 값이기 때문에 gradient도 작을 것이고 결국 업데이트가 잘 되지 않을 것이다.

 

gradient를 backprop하는 과정은

 

upstream gradient에 w의 gradient인 x를 곱한다.

 

그리고 입력 x는 어떤 내적의 결과이다.

 

backward pass의 과정에서 upstream gradient를 구하는 것은

 

현재 upstream에 가중치를 곱하는 것이다.

 

w를 계속해서 곱하기 때문에 backward pass에서도 forward 처럼 점점 gradient 값이 작아지게 된다.

 

따라서 upstream gradients는 0으로 수렴하게 된다.

 

여기서 upstream은 gradient가 흘러가는것이다.

 

loss에서부터 시작해서 최초 입력까지 흘러간다.

 

현재 노드를 계산하고 또 밑으로 흘러내려간다.

 

backprop으로 노드에 흘러 들어온 것이 upstream이다.

 

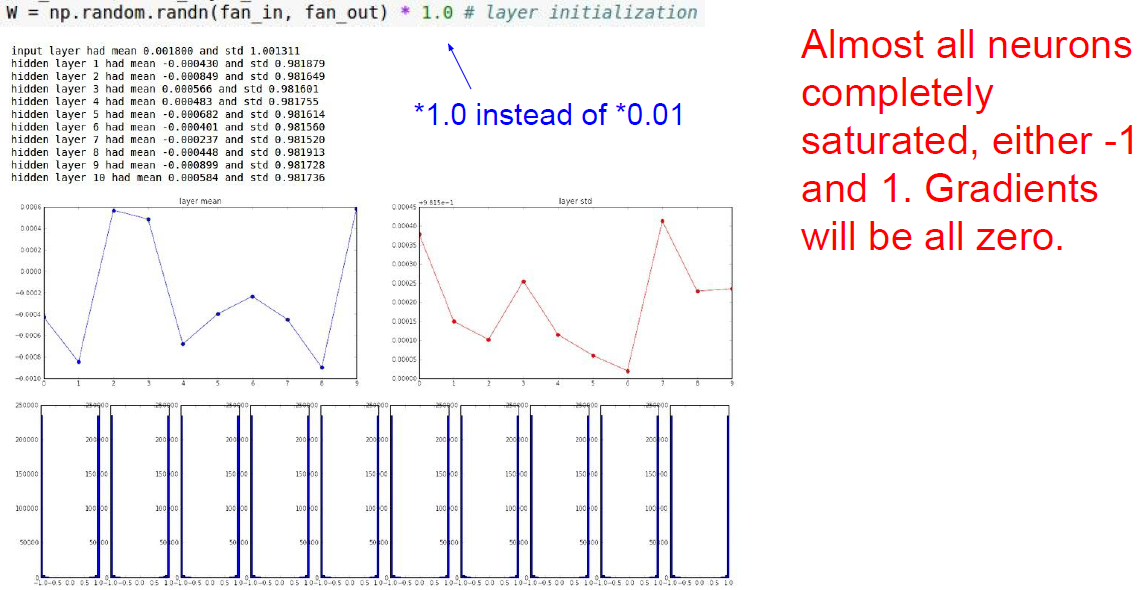
그렇다면 가중치를 좀 더 큰 값(0.01 -> 1.0)으로 초기화하면 어떨까?

 

이렇게 큰 가중치를 통과한 출력 wx를 구하고 이를 tanh를 거친다면 어떻게 될까?

 

앞서 언급했던데로 tanh에서 큰 값이 입력으로 들어오면 saturation 될 것이다.

 

그렇게되면 항상 -1 혹은 +1 일 것이다.

 

값이 saturation이 되면 gradient는 0이 되며, 가중치 업데이트가 되지 않기에 적절한 가중치를 얻기 어려워진다.

 

너무 작으면 사라져버리고, 너무 크면 saturation되어 버린다.

 

그래서 사람들이 어떻게 하면 가중치 초기화를 잘 할 수 있을까 고민했다.

 

널리 알려진 좋은 방법 중 하나는 Xavier initialization이다.

 

Glorot가 2010에 발표한 논문이다.

 

그림 위의 w 공식을 살펴보면

 

std gaussian으로 뽑은 값을 입력의 수로 scaling 해준다.

 

기본적으로 xavier initialization가 하는 일은 입력/출력의 분산을 맞춰주는 것이다.

 

입력의 수가 작으면 더 작은 값으로 나누기 때문에 좀 더 큰 값을 얻는다.

 

우리는 더 큰 가중치가 필요하다.

 

왜냐하면 작은 입력의 수가 가중치와 곱해지기 때문에

 

가중치가 더 커야만 출력의 분산 만큼 큰 값을 얻을 수 있다.

 

반대로 입력의 수가 많은 경우에는 더 작은 가중치가 필요하다.

 

하지만 문제가 하나 있다.

 

ReLU를 쓰면 잘 동작하지 않는다는 것이다.

 

ReLU는 출력의 절반을 0으로 만든다.

 

이는 결국 출력의 분산을 반토막 낸다는 것이다.

 

ReLU에서는 값이 너무 작아지기 때문에 잘 작동하지 않게 된다.

 

위의 그림은 이러한 분포가 줄어드는 현상을 나타낸다.

 

점점 더 많은 값들이 0이 되고 결국은 비활성(deactivated)된다.

 

이 문제를 해결하기 위한 논문이 있다.

 

여기서는 추가적으로 2를 더 나눠준다.

 

neuron 중 절반이 없어진다는 사실을 고려하기 위함이다.

 

실제 입력은 반밖에 안들어가므로 반으로 나워주는 텀을

 

추가적으로 더해주는 것이고 실제로 잘 동작한다.

 

실제로 2를 더 나눠주는 이 작은 변화는 학습에 있어서 큰 차이를 보인다.

 

일부 논문에서는 이러한 작은 차이가 학습이 정말 잘 되거나 아예 안되거나하는 결정하는 결과를 보이기도 한다.

 

gaussian의 범위로 activation을 유지시키는 것에 관련된 다른 아이디어를 살펴보자.

 

우리는 layer의 출력이 unit gaussian이길 원한다.

 

batch normalization은 unit gaussian 형태로 강제로 만들어보자는 아이디어이다.

 

어떤 layer로부터 나온 batch 단위 만큼의 activations가 있다고 했을 때,

 

우린 이 값들이 unit gaussian이기를 원한다.

 

현재 batch에서 계산한 mean과 variance를 이용해서 normalization 할 수 있다.

 

가중치를 잘 초기화 시키는 것 대신에

 

학습할 때 마다 각 layer에 이러한 normalization을 통해

 

모든 layer가 unit gaussian이 되도록 한다.

 

결국 학습하는 동안 모든 layer의 입력이 unit gaussian이 됐으면 좋겠다는 것이다.

 

그렇게하기 위해 네트워크의 forward pass에서

 

unit gaussian이 되도록 명시적으로 만들어준다.

 

각 neuron을 mean과 variance로 normalization 해주므로

 

이런 일을 함수로 구현하는 것이다.

 

batch 단위로 한 layer에 입력으로 들어오는 모든 값들을 이용해서

 

mean과 variance를 계산해서 normalization 해준다.

 

이렇게 만든 함수를 보면 미분이 가능하다.

 

mean과 variance를 상수로 가지고 있으면 미분이 가능해서 backprop가 가능하게 된다.

 

위 그림을 보면 batch당 N개의 학습 데이터가 있고 각 데이터가 D차원이라고 가정하자.

 

각 차원별로 mean을 각각 계산한다.

 

하나의 batch 내에 이걸 전부 계산해서 normalize한다.

 

그리고 이 BN은 FC 혹은 conv layer 다음에 넣어준다.

 

BN은 입력의 scale만 살짝 조정해주는 역할이기 때문에

 

FC와 conv 어디에든 적용할 수 있다.

 

conv layer에서 차이점이 있다면 normalization을 차원마다 독립적으로 수행하는 것이 아니라

 

같은 activation map의 같은 채널에 있는 요소들은 같이 normalize 해준다.

 

왜냐하면 conv 특성상 같은 방식으로 normalize 시켜야하기 때문이다.

 

conv layer의 경우 activation map(channel, depth) 마다 mean과 variance를 하나만 계산한다.

 

그리고 현재 batch에 있는 모든 데이터로 normalize 해준다.

 

문제는 FC를 거칠 때 마다 매번 normalization을 해주는 것이다.

 

위의 그림에서 tanh의 입력이 unit gaussian 형태가 맞는것인가?

 

normalization의 역할은 입력이 tanh의 linear한 영역에만 존재하도록 강제하는 것이다.

 

그렇게 되면 saturation이 전혀 일어나지 않게 된다.

 

하지만 saturation이 전혀 일어나지 않는것보다

 

얼마나 saturation이 일어날지를 조절하는것이 더 좋다.

 

BN은 normalization 이후 scaling 연산을 추가한다.

 

이를 통해 unit gaussian으로 normalize 된 값들을

 

감마는 scaling 효과를, 베타는 shifting의 효과를 준다.

 

이렇게 하면 normalized 된 값들을 다시 원상복구할 수 있다.

 

감마 = variance, 베타 = mean으로 하면 BN을 하기 전 값으로 돌아갈 수 있다. (오른쪽 수식)

 

네트워크에서 데이터를 tanh에 얼마나 saturation 시킬지를 학습하기 때문에 유연성을 얻을 수 있다.

 

batch normalization을 요약하면,

 

모든 mini-batch 각각에서의 mean과  variance를 계산한다.

 

그리고 mean과 variance로 normalize 한 이후에

 

다시 추가적으로 scaling, shifting factor를 사용한다.

 

BN은 gradient의 흐름을 보다 원할하게 해주며

 

결국 학습이 더 잘되게 해준다.

 

BN을 사용하면 learning rate를 좀 더 높일 수 있고

 

다양한 초기화 방법들을 사용해볼 수 있다.

 

그래서 사람들이 BN을 쓰면 학습이 더 쉬워진다고 평가한다.

 

또 한가지는 BN이 regularization의 역할도 한다는 것이다.

 

각 layer의 출력은 해당 데이터 하나 뿐만 아니라

 

batch 안에 존재하는 모든 데이터들에 영향을 받는다(mean, variance).

 

왜냐하면 각 layer의 입력은 해당 배치의 평균으로 normalize되기 때문이다.

 

그렇기 때문에 이 layer의 출력은 이제 오직 하나의 샘플에 대한

 

deterministic한 값이 아니게 되고

 

batch 내의 모든 데이터가 입력으로 한대 묶인다고 볼 수 있다.

 

그러므로 더 이상 레이어의 출력은 deterministic하지 않고

 

조금씩 바뀌게 되고 이는 regularization effect를 주게된다.

 

BN에서 mean과 variance는 학습 데이터에서 계산한다.

 

inference time에 추가적인 계산을 하지 않는다.

 

training time에서 running average 같은 방법으로

 

mean, variance를 계산하고 inference time에 사용한다.

 

이제 학습 과정을 어떻게 모니터링하고 하이퍼파라미터를 조절할 것인지 살펴보자.

 

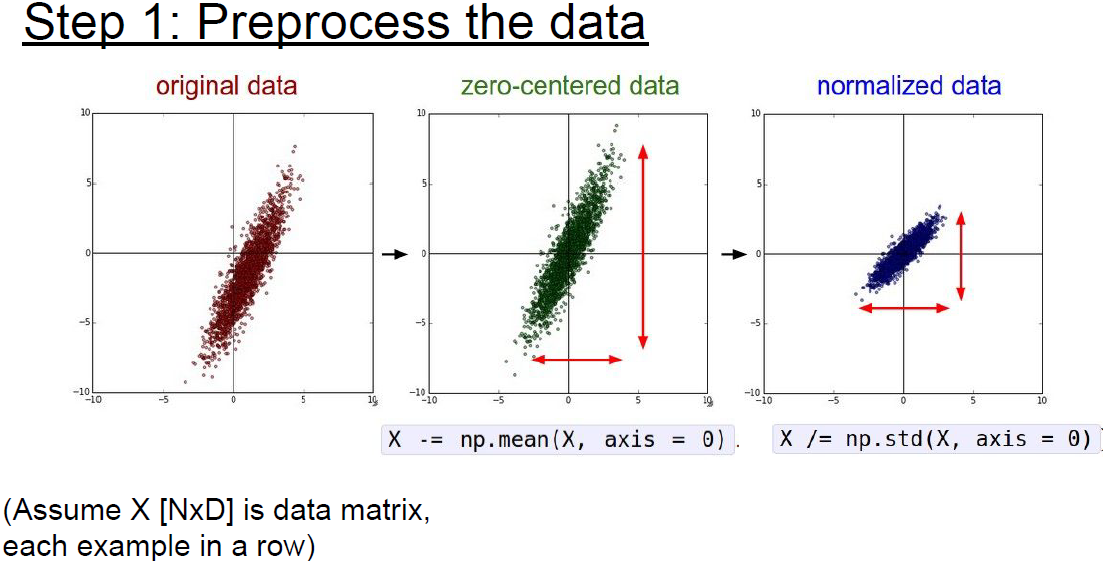
첫 단계는 데이터 전처리이다.

 

앞서 설명한대로 zero-mean을 사용한다.

 

그리고 아키텍처를 선택한다.

 

위의 그림은 하나의 hidden layer와 50개의 neuron을 가진 모델이다.

 

이후 네트워크를 초기화해야한다.

 

Forward pass를 하고 난 후에 계산된 loss가 그럴듯해야 한다.

 

만약 softmax를 사용하고자 한다면 지난 강의들을 토대로

 

가중치가 작은 값일 때 loss가 대강 어떻게 분포해야 하는지 이미 알고 있다.

 

softmax classifier의 loss는 negative log likelihood가 되어야 한다.

 

10개의 클래스라면 loss는 -log(1/10)이 될 것이다.

 

위의 그림에서 loss가 약 2.3으로 잘 동작한다는 것을 알 수 있다.

 

이러한 방법은 좋은 sanity check 방법이다.

 

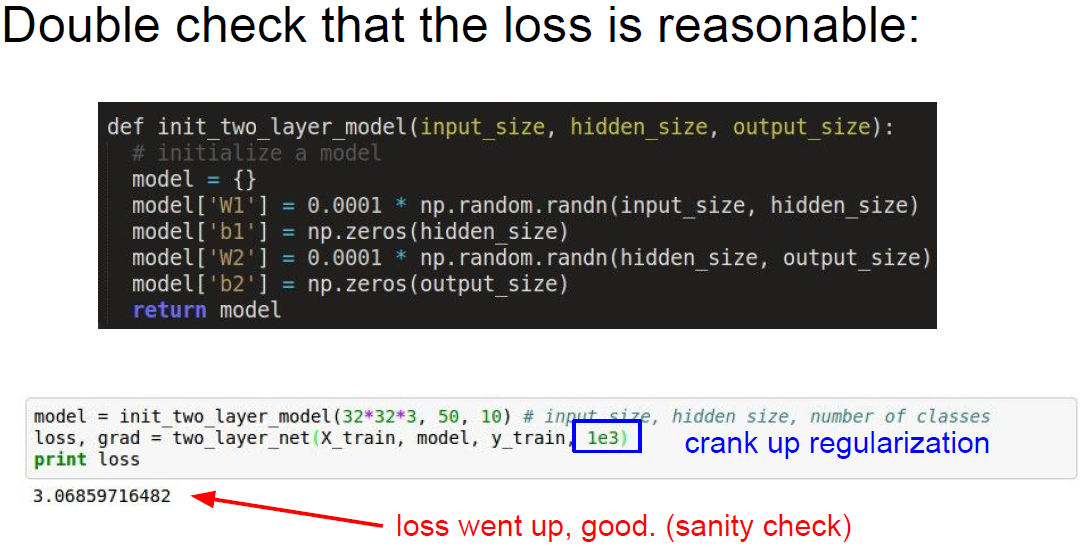
loss가 정상인것을 확인했다면 regularization term을 추가해보자.

 

이전은 regularization term을 0으로 했었는데

 

1000으로 regularization term을 추가하면 loss가 증가한다.

 

이것 또한 유용한 sanity check 방법이다.

 

처음 학습을 시작할 때 좋은 방법은 데이터의 일부만 우선 학습시켜 보는 것이다.

 

데이터가 적으면 당연히 over fitting이 생길 것이고 loss가 많이 줄어들 것이다.

 

이때는 regulaization을 사용하지 않고 loss가 내려가는지 확인한다.

 

위 그림처럼 epoch 마다 loss가 잘 내려가는지 확인한다.

 

loss가 0을 향해 꾸준히 잘 내려가는지를 확인하자.

 

loss가 감소함과 동시에 train accuracy는 점점 증가한다.

 

데이터가 작은 경우라면 모델이 완벽하게 데이터를 over fitting 할 수 있어야 한다.

 

이제는 전체 데이터셋을 사용하고 regularization을 약간만 주면서

 

적절한 learning rate를 찾아야한다.

 

learning rate는 가장 중요한 하이퍼파라미터 중 하나이다.

 

가장 먼저 정해야만 하는 하이퍼파라미터이다.

 

우선 몇 가지 정해서 실험을 해보자.

 

위의 예제에서는 1e-6으로 정했다.

 

그 결과로 loss가 크게 변하지 않는 것을 볼 수 있다.

 

loss가 잘 감소하지 않는 가장 큰 요인은 learning rate가 지나치게 작은 경우이다.

 

learning rate가 지나치게 작으면 gradient 업데이트가 충분히 일어나지 않고

 

loss가 변하지 않는다.

 

여기서 유심히 살펴봐야할 점은 loss가 잘 변하지 않음에도

 

training 및 validation accuracy가 20%가지 상승하였다.

 

위의 epoch 마다 확률 값들이 멀리 퍼져있기 때문에 loss가 비슷비슷한 결과를 보인다.

 

하지만 학습을 통해 확률이 조금씩 옮은 방향으로 바뀌기 때문에 

 

가중치는 조금씩 바뀌지만 accuracy는 갑자기 증가할 수 있는 것이다.

 

learning rate를 좀 크게 바꿔보자.

 

1e-6에서 1e6으로 바꿔서 학습한 결과를 살펴보자.

 

결과를 보면 loss가 NaNs임을 볼 수 있다.

 

NaNs는 loss가 발산(exploded)한 것이다.

 

주된 이유는 learning rate가 지나치게 높기 때문이다.

 

이 경우에는 learning rate를 낮춰야만 한다.

 

그래서 3e-3으로 바꿔지만 여전히 발산한다.

 

보통 learning rate는 1e-3에서 1e-5 사이의 값을 사용한다.

 

이 범위의 값을 이용해서 cross-validation을 수행한다.

 

이 사이의 값들을 이용해서 learning rate가 지나치게 작은지 큰지를 결정할 수 있다.

 

그럼 하이퍼파라미터는 어떻게 정해줘야 할까?

 

하이퍼파라미터를 최적화시키고 그 중 가장 좋은 것을 선택하려면 어떻게 해야 할까?

 

한 가지 전략은 cross-validation이다.

 

cross-validation은 training set으로 학습시키고 validation set으로 평가하는 방법이다.

 

우선 coarse stage에서는 넓은 범위에서 값을 골라낸다.

 

epoch 몇 번 만으로도 현재 값이 잘 동작하는지 알 수 있다.

 

epoch가 많지 않아도 어떤 하이퍼파라미터가 좋은지 나쁜지를 알 수 있다.

 

NaN이 뜨거나 혹은 loss가 감소하지 않거나 하는 것을 확인하면서

 

적절히 잘 조절할 수 있을 것이다.

 

coarse stage가 끝나면 어느 범위에서 잘 동작하겠다는것을 대충 알 수 있다.

 

두 번째 fine stage에서는 좀 더 좁은 범위를 설정하고

 

학습을 좀 더 길게 시켜보면서 최적의 값을 찾는다.

 

NaNs로 발산하는 징조를 미리 감지할 수도 있다.

 

학습하는 동안 loss가 어떻게 변하는지를 살펴보는 것이다.

 

이전의 loss 보다 더 커진다면 (많이)

 

잘못되고 있다는 것이다.

 

이럴때는 다른 하이퍼파라미터를 선택해야한다.

 

위의 예시는 5 epoch을 돌며 coarse search를 하는 과정이다.

 

여기서 확인해야하는 것은 validation accuracy이다.

 

높은 val acc는 빨간색으로 표시되어있다.

 

이 빨간색 구간이 바로 fine-stage를 시작할만한 범위가 된다.

 

한 가지 주목할 점은 하이퍼파라미터 최적화시에는

 

regularization term과 learning rate를 log scale로 값을 주는 것이 좋다.

 

파라미터 값을 샘플링할때 10^-3 ~ 10^-6을 샘플링하지 말고

 

10의 차수 값만 샘플링하는 것이 좋다. (-3 ~ -6)

 

왜냐하면 learning rate는 gradient와 곱해지기 때문에

 

learning rate 선택 범위를 log scale을 사용하는 편이 좋다.

 

따라서 차수(orders of magnitute)를 이용하는 것이 좋다.

 

범위를 다시 한번 조절해보자. (오른쪽 그림)

 

reg는 범위를 10^-4에서 10^0 정도로 좁히면 좋을 것 같다.

 

val_acc 중간 범위에서 53%의 val_acc를 보이는 것을 볼 수 있다.

 

학습이 가장 잘 되는 구간일것이다.

 

그러나 문제가 있다.

 

아래에 있는 빨간색 박스는 가장 좋은 acc를 보인다. (0.531)

 

해당되는 learning rate들을 보면 전부 10e-4 사이에 존재하고 있다.

 

learning rate의 최적 값들이 우리가 다시 범위를 좁혀 설정한 범위의

 

경계부분에 집중되어 있다는 것을 알 수 있다.

 

이렇게 되면 최적의 learning rate를 효율적으로 탐색할 수 없을수도 있다.

 

실제 최적의 값이 1e-5 혹은 1e-6 근처에 존재할수도 있다.

 

탐색 범위를 조금만 이동시키면 더 좋은 범위를 찾을 수 있을지도 모른다.

 

여기서 우리는 최적의 값이 내가 정한 범위의 중앙 쯤에 위치하도록

 

잘 설정해주는것이 중요하다.

 

하이퍼파라미터를 찾는 또 다른 방법은 grid search를 이용하는 것이다.

 

하이퍼 파라미터를 고정된 값과 간격으로 샘플링하는 것이다.

 

하지만 실제로 grid search 보다는 random search를 하는 것이 더 좋다.

 

random search를 하는 경우는 오른쪽 그림과 같다.

 

random이 더 좋은 이유는

 

내 모델이 어떤 특정 파라미터의 변화에 더 민감하게 반응을 하고 있다고 생각해보면 (노랑 < 초록)

 

이 함수가 더 비효율적인 dimentionality를 보인다고 할 수 있으며 (노랑에는 별 영향을 받지 않음)

 

random search는 중요한 파라미터(초록)에게도 더 많은 샘플링이 가능하므로

 

위에 그려놓은 초록색 함수를 더 잘 찾을 수 있다.

 

grid layour에서는 오직 세 번의 샘플링 밖에 할 수 없으므로

 

good region이 어디인지 제대로 찾을 수 없다.

 

random search를 사용하면 important variable에서 더 다양한 값을 샘플링할 수 있다.

 

실제 우리는 하이퍼파라미터 최적화와 cross-validation을 많이 해야한다.

 

많이 해서 많은 하이퍼파라미터를 직접 돌려보고 모니터링해서 어떤 값이 좋고 나쁜지를 확인해야 한다.

 

loss curve를 보면서 좋은 것을 찾아서 시도해보는 일을 계속 반복해야 한다.

 

loss curve를 모니터링 하는데 있어서 learning rate가 정말 중요하다.

 

loss curve를 보고 어떤 learning rate가 좋고 나쁜지를 알아볼 수 있다.

 

loss가 발산하면 learning rate가 높은 것이고

 

너무 평평(linear)하면 낮은 것이다.

 

가파르게 내려가다가 어느 순간 정체기가 생기면

 

이 또한 여전히 너무 높다는 의미이다.

 

learning step이 너무 크게 점프해서 적절한 local optimum에 도달하지 못하는 경우이다.

 

최적의 learning rate에 대한 loss curve는 왼쪽 그림과 같다.

 

비교적 가파르게 내려가면서도 지속적으로 잘 내려간다면 현재 learning rate를 유지해도 좋다.

 

loss가 평평하다가 갑자기 가파르게 내려간다면

 

이는 초기화 문제일수있다.

 

gradient의 backprop이 초기에는 잘 동작하지 못하다가 학습이 진행되면서 회복이 되는 경우이다.

 

위의 그림은 accuracy를 모니터링하면 볼 수 있는 현상이다.

 

train acc와 val acc가 큰 차이를 보인다면 over fitting일수도 있다.

 

따라서 regularization 강도를 높여야 될 수 있다.

 

큰 차이가 없다면 아직 overfitting 하지 않은 것이고 capacity를 높일 수 있는 여유가 있는 것을 의미한다.

 

가중치의 크기 대비 가중치 업데이트의 비율을 확인할 필요도 있다.

 

먼저 파라미터의 norm을 계산해서 가중치의 규모를 계산한다.

 

그리고 norm을 통해 업데이트 사이즈를 계산할 수 있고

 

얼마나 크게 업데이트 되는지를 알 수 있다.

 

우리는 이 비율이 대략 0.001 정도 되길 원한다.

 

이 값은 변동성이 커서 정확하지 않을 수 있다.

 

하지만 업데이트가 지나치게 크거나 작은지에 대한 감을 어느정도 가질 수 있다.

 

업데이트가 너무 지나치거나 아무런 업데이트도 없으면 안된다.

1957년에 Frank Rosenblatt가 Mark I Perceptron Machine을 개발했다.

 

최초의 perceptron을 구현한 기계이다.

 

perceptron은 wx+b와 유사한 함수를 사용한다.

 

왜 똑같은게 아니고 유사하냐면 출력값이 1 또는 0이기 때문이다.

 

가중치 w는 update rule이 존재한다.

 

하지만 이것은 w를 조절하면서 맞추는 식이였다.

 

1960년대에는 Widrow와 Hoff가 Adaline과 Madaline을 개발했다.

 

이것은 최초의 multilayer perceptron network를 구현한 기계였다.

 

하지만 backpropagation과 같은 알고리즘은 없었다.

 

최초의 backpropagation은 1986년에 Rumelhart가 제안했다.

 

chain rule과 update rule을 확인할 수 있다.

 

이때가 최초로 network를 학습시키는 개념이 정립되기 시작했다.

 

2006년에 RBM을 통해 DNN의 학습 가능성을 보여줬다.

 

하지만 이때까지도 모던한 NN은 아니였다.

 

backpropagation을 수행하려면 세심한 초기화가 필요했다.

 

초기화를 위해 전처리 과정이 필요했고

 

각 히든레이어 가중치를 학습해야했다.

 

이렇게 초기화된 히든 레이어를 이용해서

 

전체 신경망을 backpropagation 하거나 fine tune을 수행했다.

 

실제로 NN이 유명세를 타기 시작한 때는 2012년부터이다.

 

NN이 음성 인식에서 아주 좋은 성능을 나타냈기 때문이다.

 

또한 2012년에 영상 인식 관련해서도 유명한 AlexNet이 나온다.

 

이 논문은 ImageNet classification에서 최초로 NN을 사용했고 결과는 굉장했다.

 

AlextNet은 ImageNet benchmark의 error를 그때 당시 극적으로 감소시켰다.

 

이후 ConvNet은 널리 쓰이고 있다.

 

다시 1950년대로 돌아가 Hubel & Wiesel이 일차 시각피질의 뉴런에 관한 연구를 수행한 것을 떠올려보자.

 

고양이 뇌에 전극을 꼽아서 다양한 자극을 주고 실험을 진행했다.

 

여기서 뉴런이 oriented edge와 shape와 같은 것들에게 반응한다는 것을 알게 되었다.

 

고양이 실험에서 내린 중요한 결론 중 하나는

 

피질(cortex) 내부에 topograhical mapping이 존재한다는 것이다.

 

피질 내 서로 인접해 있는 세포들은 visual field에서 지역성을 나타낸다.

 

위의 오른쪽 그림을 보면 해당되는 spatial mapping을 볼 수 있다.

 

쉽게 말하면 눈으로 본거를 피질에서 공간적으로 표현된다고 볼 수 있다.

 

또 다른 중요한 점은 뉴런들이 계층 구조를 지니고 있다는 점이다.

 

다양한 종류의 시각 자극에 대해 시각 신호가 가장 먼저 도달하는 위치가

 

망막으로부터 시각적인 정보를 뇌로 전달하는 망막절 세포(retinal ganglion cell)이라는 것을 발견했다.

 

가장 상위에는 simple cell들이 있는데

 

다양한 edge의 방향과 빛의 방향에 대해 반응을 나타냈다.

 

그리고 simple cell이 complex cell과 연결되어 있다는 것을 발견했다.

 

complex cell은 빛의 방향 뿐만 아니라 움직임에 대해서도 반응을 나타냈다.

 

복잡도가 증가한 hypercomplex cell들은

 

끝 점(end point)에 반응하는 것을 나타냈다.

 

이러한 발견들로부터 corner나 blob에 대한 아이디어를 얻기 시작했다.

 

1980년에 Neocognitron은 Hubel & Wiesel의

 

simple/complex cell 아이디어를 사용한 최초의 NN이다.

 

simple/complex cell을 교차시켰다.

 

simple cell은 학습 가능한 파라미터를 가지고 있었고,

 

complex cell은 pooling과 같은 역할로 구현했으며 작은 변화에 simple cell보다 좀 더 강인하다.

 

지금가지 1980년대까지의 업적을 살펴보았다.

 

1998년 Yann LeCun이 최초로 NN을 학습시키기 위해 backpropagation과

 

gradient-based learning을 적용했다.

 

이 방법은 우체국에서 문자 인식과 숫자 인식에 쓰였으며 잘 동작했다.

 

하지만 네트워크를 더 크게 만들지 못했고 숫자 데이터는 단순했다.

 

 

2012년 AlexNet이 CNN의 현대화를 불러 이르켰다.

 

이는 Yann LeCun의 CNN과 크기 다르지 않고 단지 더 크고 깊어졌다.

 

또한 ImageNet과 같은 대량의 dataset을 활용할 수 있었으며 GPU를 활용할 수 있었다.

 

오늘날 ConvNets 어디에서나 쓰인다.

 

AlexNet의 ImageNet classification 결과를 보면 이미지 검색(retrieval)에 좋은 성능을 보인다.

 

위의 그림에서 오른쪽 그림을 보면 유사한 특징을 매칭시키는데 탁월하다는 것을 알 수 있다.

 

Detection에서도 ConvNet을 사용한다.

 

이미지에서 객체를 찾고 bounding box를 그린다.

 

segmentation도 수행할 수 있다. 이는 bbox만 치는게 아니라

 

객체를 구별하는데 픽셀 하나하나를 classification한다.

 

ConvNets은 자율주행 자동차에도 활용될 수 있다.

 

대부분 작업을 GPU가 수행하며, 병렬처리를 통해 ConvNet을 효과적으로 학습하고 추론할 수 있다.

 

임베디드 시스템에서도 동작하며, 최신 GPU에서도 가능하다.

 

위 그림은 ConvNet을 활용한 다양한 어플리케이션의 예를 보여준다.

 

ConvNet을 단일 이미지와 시간적 정보를 이용하여 비디오에도 활용할 수 있다.

 

pose estimation도 가능하다.

 

어깨나 팔꿈치와 같은 다양한 관절 포인트를 인식할 수 있다.

 

사람의 비정형적인 포즈를 잘 검출하는 것을 볼 수 있다.

 

강화학습을 통해 게임을 하거나 바둑을 두는것도 가능하다.

 

이러한 여러 작업들에서 ConvNet은 아주 중요한 역할을 한다.

 

또 다른 예로는 의료 영상을 가지고 해석하거나 진단을 하는데 활용되는 것이다.

 

우주 은하를 분류하거나 표지판을 인식할수도 있다.

 

Kaggle Chanllange에서 고래를 분류하는 작업도 있었다.

 

항공 지도를 활용하여 길과 건물 인식을 수행할 수 있다.

 

classification과 detection에서 좀 더 나아가 image captioning을 수행할 수 있다.

 

image captioning은 해당 이미지의 설명을 문장으로 생성한다.

 

또한 Neural Network를 이용해서 멋진 예술작품도 만들어 낼 수 있다.

 

위의 그림 왼쪽은 Deep Dream 알고리즘의 결과를 나타낸다.

 

오른쪽 그림은 style transfer라는 방법은 원본 이미지를 가지고 특정 화풍으로 다시 그려주는 알고리즘이다.

 

오른쪽 하단 그림은 원본 주택 이미지를 반 고흐의 별이 빛나는 밤의 화풍으로 바꾼것이다.

 

CNN에 대해 어떻게 동작하는지 알아보자.

 

우선 FC를 살펴보자.

 

위의 그림에서 32x32x3의 이미지를 입력으로 활용했다.

 

이 이미지를 길게 펴서 3072-dim의 벡터로 만들었다.

 

그리고 10x3072 크기의 가중치 W와 곱하면(Wx) activation을 얻을 수 있다.

 

activation은 10개의 행으로 되어 있으며 3072-dim 입력과 가중치 W를 내적한 결과를 나타낸다.

 

그러면 어떤 하나의 숫자를 얻을 수 있는데 이는 neuron 중 하나의 값이라고 할 수 있다.

 

위 예시는 10개의 출력이 있는 경우이다.

 

conv layer와 FC layer의 주요 차이점은

 

conv layer는 기존의 spatial 구조를 보존한다는 것이다.

 

기존의 FC layer가 입력 이미지를 길게 폈다면

 

conv layer는 이미지 구조를 그대로 유지한다.

 

위의 그림에서 파란색 작은 필터가 가중치 W가 된다.

 

5x5x3 필터가 이미지를 슬라이딩하면서 공간적으로 내적(dot product)을 수행한다.

 

필터는 항상 입력의 깊이(depth)만큼 확장된다. (입력 깊이 3, 필터 깊이 3)

 

위의 예제는 32x32 이미지에 필터 크기가 5x5이지만

 

depth를 보면 입력의 전체 depth를 취한다. 여기서는 5x5x3이 된다.

 

이 필터 w를 가지고 전체 이미지에 내적을 수행한다.

 

필터 w와 이에 해당하는 이미지의 픽셀을 곱한다.

 

필터의 크기가 5x5x3이 의미하는 것은 그 만큼 곱셈연산을 수행한다는 의미이다. (5x5x3 = 75)

 

추가로 bias term이 하나 있을 수 있다.

 

w에 transpose를 한 이유는 행벡터(1x75)를 만들어 내적을 하기 위한 것이다.

 

convolution은 이미지의 좌측 상단부터 필터가 슬라이딩하면서 수행된다.

 

필터의 모든 요소를 가지고 내적을 수행하게 되면 하나의 값을 얻을 수 있다.

 

그리고 슬라이딩을 해서 반복한다.

 

이렇게 나온 값들을 output activation map의 해당 위치에 저장한다.

 

위의 그림에서 입력 이미지와 출력 activation map의 차원(dim)이 다른것을 볼 수 있다.

 

입력은 32x32이고 출력은 28x28이다.

 

출력 크기는 슬라이딩을 어떻게 하느냐에 따라 달라질 수 있지만 보통 1씩 건너서 슬라이딩한다.

 

또 다른 하나의 필터를 이용하여 전체 이미지에 convolution 연산을 수행한다.

 

또 다른 같은 크기의 activation map을 얻게된다.

 

보통 이처럼 여러개의 필터를 이용한다.

 

왜냐하면 필터마다 다른 특징을 추출하기 위함이다.

 

하나의 Layer에서 원하는 만큼의 필터를 사용할 수 있다.

 

위 그림에서는 5x5x3크기의 필터 6개를 사용했다

 

CNN은 보통 conv layer의 연속된 형태를 이룬다.

 

각각 conv layer를 쌓아 올리면 linear layer로 된 NN이 된다.

 

그 사이에 ReLU같은 activation function을 추가하여 비선형성을 만든다.

 

이렇게 되면 conv-relu가 반복되고 중간중간에 pooling layer도 들어간다.

 

그리고 각 layer 출력은 다음 layer의 입력이 된다.

 

각 layer는 여러개의 필터를 가지고 있고 각 필터마다 각각의 activation map을 만든다.

 

이런식으로 여러개의 layer를 쌓으면 각 필터들을 계층적으로 학습할 수 있다.

 

앞쪽에 있는 필터들은 edge와 같은 low level feature를 학습한다.

 

mid level feature를 보면 corner나 blob과 같은 좀 더 복잡한 특징을 가지게 된다.

 

high level feature를 보면 객체와 비슷한 것들을 특징으로 가지는 것을 볼 수 있다.

 

이는 layer의 계층에 따라 단순하거나 복잡한 특징을 뽑는다는것을 보여준다.

 

이러한 현상은 Hubel & Wiesel의 이론과도 잘 맞는다.

 

네트워크 앞단에는 단순한 작업을 처리하고 뒤로 갈수록 점점 더 복잡해지는것이다.

 

이러한 현상은 강제로 학습시킨것이 아니라

 

계층적 구조를 설계하고 역전파로 학습을 시켜서 나온 결과이다.

 

여러개의 각 필터는 이런식으로 학습이 된다.

 

위의 그림은 5x5 필터의 출력인 activation map의 visualization한것이다.

 

상단의 작은 그림은 5x5 필터가 어떻게 생겼는지 보여준다.

 

입력 이미지는 자동차의 헤드라이트 부분이다.

 

빨간 네모박스를 보면 edge를 찾고 있다.

 

이 필터를 슬라이딩 시키면 이 필터와 비슷한 값들은 값이 커지게 된다. (하단 빨간 네모박스)

 

이미지 중 어느 위치에서 각 필터가 크게 반응하는지 알 수 있다.

 

CNN은 입력 이미지를 여러 layer에 통과시킨다.

 

첫 번째 conv layer후에 ReLU non-linear layer를 통과한다.

 

conv-relu-conv-relu를 수행한 뒤 pooling layer를 통과한다.

 

pooling은 activation map 사이즈를 줄이는 역할을 한다.

 

CNN 끝단에는 FC layer가 있다.

 

conv layer 마지막 출력과 연결되어 최종 스코어를 계산한다.

 

32x32x3 이미지가 있고 5x5x3 필터를 가지고 연산을 수행한다고 생각해보자.

 

왜 출력이 28x28이 나오게 될까?

 

간단한 예시로 7x7 입력에 3x3 필터가 있다고 가정해보자.

 

이미지 좌측상단부터 필터를 슬라이딩하면서 내적을 수행한다.

 

내적의 출력 값들은 activation map의 좌측 상단부터 저장된다.

 

다음 단계를 필터를 오른쪽으로 한칸 슬라이딩한다.

 

그럼 또 하나의 내적 값을 얻을 수 있다.

 

이런식으로 반복하다보면 결국 5x5의 activation map을 얻을 수 있다.

 

이 필터는 좌우 방향과 상하방향으로 5번씩만 슬라이딩할 수 있다.

 

슬라이딩을 두 칸씩 움직일수도 있다.

 

여기서 움직이는 칸을 stride라고 한다. stride를 2로 설정하면 슬라이딩을 2칸씩 건너뛰면서 하는 것이다.

 

그럼 결국 3x3 activation map을 얻게될것이다.

 

그렇다면 stride가 3일때 출력 사이즈는 몇이 될까?

 

이때는 필터가 이미지를 슬라이딩해도 모든 이미지를 커버할 수 없게된다.

 

이렇게되면 데이터 손실도 있고 불균형한 결과를 볼 수 있다.

 

위의 그림은 상황에 따라 출력 사이즈가 어떻게 되는지 계산할 수 있는 수식을 나타낸다.

 

입력의 차원이 N이고 필터 사이즈가 F이고 stride가 주어지면 출력 크기는 (N-F) / stride + 1이 된다.

 

이를 이용해서 어떤 필터 크기를 사용해야 하는지 알 수 있다.

 

또한 어떤 stride를 사용했을때 이미지에 맞는지, 몇 개의 출력값을 낼 수 있는지도 알 수 있다.

 

출력 사이즈를 입력 사이즈와 동일하게 만들기 위한 방법 중

 

흔히 쓰이는 방법이 zero padding이다.

 

이미지의 경계를 포함할 수 있는 방법이기도 하다.

 

zero pad는 이미지의 가장자리에 0을 채워 넣는다.

 

이렇게되면 왼쪽 상단 끝부터 conv 필터 연산을 수행할 수 있다.

 

7x7입력에 3x3필터 연산시 zero padding을 넣는다면 출력은 7x7이 된다.

 

일반적으로 필터 크기가 3일때 zero pad는 1로,

 

5일때 2로, 7일때 3을 사용한다.

 

여러 layer를 계층적으로 쌓을때 zero padding을 하지 않는 다면

 

출력 사이즈가 계속 줄어들것이다.

 

깊은 네트워크가 있다면 activation map은 계속 줄어들고 엄청 작아진다.

 

그렇게되면 일부 정보를 잃게 될것이고 원본 이미지를 표현하기에는 너무 작은 값을 사용하게 된다.

 

출력 크기가 줄어드는 이유는 입력의 가장자리를 계산하지 못하기 때문이다.

 

입력 이미지 크기가 32x32x3이고 5x5x3 필터 10개 있다.

 

여기서 stride를 1로 하고 padding을 2로 했을때 출력사이즈는 몇이 될까?

 

입력 사이즈 F가 32가 되고 padding으로 2씩 증가시키면 32+4 = 36이된다.

 

여기서 필터 사이즈 5를 빼고 stride 1로 나누고 1을 더하면 각 필터는 32x32가 된다.

 

전체 필터 개수는 10개로 10개의 activation map이 만들어진다.

 

그럼 전체 출력 크기는 32x32x10이 된다.

 

그럼 파라미터는 총 몇개일까?

 

하나의 필터는 5x5x3개의 파라미터가 있고 하나의 bias를 가질 수 있다. 75 + 1 = 76

 

이러한 필터가 10개기 때문에 총 파라미터의 개수는 76 * 10 = 760개이다.

 

위의 그림은 conv layer의 요약이다.

 

일반적인 필터 사이즈로 3x3, 5x5를 사용한다.

 

stride는 1이나 2를 많이 쓴다.

 

padding은 설정에 따라 조금씩 다르다.

 

보통 필터 개수는 32, 64, 128, 512처럼 2의 제곱수로 설정한다.

 

1x1 convolution은 depth를 조절할때 활용된다.

 

1x1은 3x3이나 5x5 등 처럼 공간적인 정보를 이용하지는 않는다.

 

하지만 depth 만큼은 연산을 수행한다.

 

그렇기 때문에 1x1 conv는 입력 전체의 depth에 대한 내적을 수행하는것과 같다.

 

위의 그림은 입력이 56x56x64이다. 여기서 32개의 1x1x64 convolution을 수행하면

 

56x56x32 크기의 activation map이 생성된다.

 

conv layer를 뇌의 neuron관점에 생각해보자.

 

오른쪽 그림은 내적과 같은 아이디어를 나타낸다.

 

입력 x가 들어오면 가중치 w와 곱한다. w는 필터값이라고 할 수 있다.

 

이는 하나의 값을 출력한다.

 

그렇지만 가장 큰 차이점은 neuron이 local connectivity를 가지고 있다는 점이다.

 

conv layer 처럼 슬라이딩을 하는것이 아니라 특정 부분에만 연결되어 있다.

 

하나의 neuron이 한 부분만 처리하고, 이러한 neuron들이 모여서 전체 이미지를 처리한다.

 

이런식을 spatial 구조를 유지한채로 layer의 출력인 activation map을 만든다.

 

5x5 필터는 각 neuron의 receptive field가 5x5라고 할 수 있다.

 

receptive field는 하나의 neuron이 한 번에 수용할 수 있는 영역을 의미한다.

 

여기서 필터가 5개라고 가정한다. (5x5x5)

 

출력값은 위 그림에서 파란색 volume처럼 생긴다.

 

출력의 크기는 28x28x5인 3D grid가 된다.

 

여기서 어떤 한 점을 찍어서 depth 방향으로 바라보면 

 

이 5개의 점은 정확하게 같은 지역에서 추출된 서로 다른 특징이라고 볼 수 있다.

 

각 필터는 서로 다른 특징을 추출한다.

 

그렇기 때문에 각 필터는 이미지에서 같은 지역을 슬라이딩하더라도

 

서로 다른 특징을 뽑는다고 할 수 있다.

 

pooling layer는 representation을 더 작게 하고 더 관리하기 쉽게 해준다.

 

즉, 파라미터 수를 줄이는 것이다.

 

공간적 불변성(invariance)를 얻을 수 있다.

 

pooling layer의 역할은 심플하다. 바로 downsampling하는 것이다.

 

예를 들어 224x224x64의 입력이 있다면 pooling을 통해 112x112x64로 '공간적으로' 줄여준다.

 

depth에는 아무런 영향이 없다.

 

최대값을 뽑는 max pooling이 일반적으로 쓰인다.

 

pooling에도 필터의 크기를 정할 수 있다.

 

필터의 크기는 얼만큼의 영역을 한번에 묶을지 정하는것이다.

 

위의 그림에서 왼쪽은 4x4 입력이고 여기에 stride 2의 2x2 max pooling을 수행하면

 

오른쪽 그림과 같이 계산된다.

 

conv layer처럼 슬라이딩하면서 연산한다.

 

max pooling이기 때문에 conv처럼 내적이 아니라 필터 안에서 가장 큰 값 하나를 뽑는다.

 

왼쪽 빨간색 영역을 보면 6이 가장 크고 녹생 영역은 8이 가장 크다.

 

노란색 영역은 3, 파란색 영역은 4가 가장 크다.

 

pooling을 수행할때는 겹치지 않게 슬라이딩하는것이 일반적이다.

 

최근은 pooling보다 stride를 이용하여 downsampling을 수행한다.

 

좀 더 좋은 성능을 나타낸다고 한다.

 

pooling layer는 입력이 W(width), H(height), D(Depth)라고 할때

 

필터 size를 정해줄 수 있다.

 

여기에 stride까지 정해주면 앞에서 언급한

 

conv layer에서 사용했던 수식을 그대로 이용할 수 있다.

 

(W - Filter Size) / Stride + 1 이 된다.

 

pooling layer는 padding을 수행하지 않는다.

 

왜냐하면 pooling의 목적은 downsampling이고 

 

conv layer처럼 가장자리 값을 계산 못하는 경우가 없기 때문이다.

 

일반적으로 pooling 필터 사이즈는 2x2, 3x3이며, 

 

stride는 보통 2로 한다.

 

conv layer가 있고 비선형성인 activation function ReLU layer를 통과한다.

 

downsampling을 할 때는 pooling layer를 섞어준다.

 

마지막에는 FC layer가 있다.

 

FC의 입력으로 사용되는 마지막 conv layer의 출력은 3차원 volume으로 이루어진다.

 

이 값들을 전부 1차원 벡터로 만들어서 FC layer의 입력으로 사용한다.

 

이렇게되면 ConvNet의 모든 출력을 서로 연결하게 되는것이다.

 

마지막 FC layer부터는 공간적 구조(spatial structure)를 신경쓰지 않게된다.

 

전부 하나로 통합시켜서 최종적인 추론을 수행한다.

 

그렇게 되면 score가 출력으로 나오게 된다.

 

최근은 pooling이나 FC layer를 점점 없애는 추세이다.

 

conv layer만 깊게 쌓는 것이다.

analytic gradient를 어떻게 계산할까?

 

computational graph를 이용하면 어떠한 함수도 표현이 가능하다.

 

위 그림에서 각 노드는 연산 단계를 나타내며,

 

input이 x, w인 선형 classifier를 보여준다.

 

곱셉 노드는 행렬 곱셈을 나타내며, 데이터 x와 가중치 w의 곱을 통해 score vector를 출력한다.

 

그 다음 hinge loss라는 계산 노드가 있다.

 

loss를 계산하는데 하단에 regularization 노드가 더해져서 최종 loss가 된다.

 

이렇게 computational graph를 이용하여 함수를 표현하면,

 

gradient를 계산하기 위해 computational graph 내부의 모든 변수에 대해

 

chain rule을 재귀적으로 사용하는 backpropagation을 사용할 수 있다.

 

computational graph는 복잡한 함수를 이용하여 작업할때 유용하다.

 

위의 AlexNet(CNN)은 top에 input image가 들어가고

 

bottom에 loss가 계산된다.

 

top에서 bottom까지 많은 layer를 거치게 된다.

 

복잡한 구조를 computational graph로 표현했다고 상상해보자.

 

graph가 매우 복잡해보일 수 있겠지만

 

결국은 풀리게 된다.

 

위의 그림은 간단한 backpropagation의 예시이다.

 

일단 함수가 있다. f(x, y, z) = (x+y)z

 

그리고 f에 대한 어떤 변수의 gradient를 알고 싶은 것이다.

 

위 함수 f를 computational graph로 표현하면 오른쪽 그림과 같다.

 

x, y에 대해 덧셈 노드가 있고 z와의 곱셈 노드가 있다.

 

여기에 예시로 값을 전달한다. x = -2, y = 5, z = -4

 

x + y 덧셈 노드를 q로 정의하면 f = q x z가 된다.

 

값을 기준으로 각 노드를 계산하면 q = 3, f = -12가 된다.

 

x와 y 각각에 대한 q의 gradient는 덧셈 노드이기 때문에 1이 된다. (수학 카테고리 참조)

 

q와 z 각각에 대한 f의 gradient는 곱셈 노드이기 때문에 각각 z와 q가 된다. (수학 카테고리 참조)

 

우리는 x, y, z 각각에 대한 f의 gradient를 알고 싶다.

 

앞서 말했듯이 backpropagation은 chain rule의 재귀적 응용이다.

 

chain rule에 의해 뒤에서부터 계산이 된다.

 

위의 그림에서 볼 수 있듯이 f에 대한 gradient는 1이 된다.

 

다음은 z에 대한 gradient를 계산해보자.

 

z에 대한 f의 미분은 q이다. (파란색 박스 오른쪽)

 

q의 값은 3이기 때문에 z에 대한 f의 미분값은 3이 된다.

 

미분값은 빨간색으로 초록색 값 하단에 표시됨.

 

다음은 q에 대한 f의 미분으로 정답은 z이다.

 

z의 값은 -4이기 때문에 q에 대한 f의 미분값은 -4가 된다.

 

이제 y에 대한 f의 미분값을 알아보자.

 

그런데 y는 f에 바로 연결되어 있지 않다.

 

f는 z와 연결되어 있다. chain rule을 이용하여 계산할 수 있다.

 

chain rule에 의해 y에 대한 f의 미분은

 

q에 대한 f의 미분과 y에 대한 q의 미분의 곱으로 나타낼 수 있다.

 

q에 대한 f의 미분은 z이고, y에 대한 q의 미분은 1이기 때문에

 

-4 * 1로 y에 대한 f의 미분값은 -4인것을 알 수 있다.

 

같은 방법으로 x에 대한 f의 미분은

 

q에 대한 f의 미분과 x에 대한 q의 미분의 곱으로 나타낼 수 있다.

 

q에 대한 f의 미분은 마찬가지로 -4가 되고, x에 대한 q의 미분 또한 1이 되기 때문에

 

-4 * 1로 x에 대한 f의 미분값 역시 -4인 것을 확인할 수 있다.

 

computational graph는 모든 노드를 표현한다.

 

하지만 각 노드는 각 노드와 각 노드에 연결된 local 입력만 알고 있다.

 

위의 예시에서의 local 입력은 x, y이고 출력은 z가 된다.

 

위의 노드에서 우리는 local gradient를 계산할 수 있다. (빨간색 박스)

 

x에 대한 z의 gradient, y에 대한 z의 gradient를 계산할 수 있다.

 

 

최종 loss L이 이미 정해져 있고

 

여기에서 z에 대한 L의 gradient를 나타낼 수 있다.

 

이제 x와 y의 값에 대한 gradient를 계산해보자.

 

chain rule을 이용하면 z에 대한 L의 미분값과 x에 대한 z의 미분값의 곱으로 계산할 수 있다.

 

여기서 x에 대한 z의 미분값은 x에 대한 z의 local gradient이므로

 

z에 대한 gradient와 local gradient의 곱으로 표현할 수 있다.

 

마찬가지로 y의 gradient는

 

z에 대한 L의 미분값과 y에 대한 z의 미분값의 곱으로 계산할 수 있다.

 

여기서 y에 대한 z의 미분값은 y에 대한 z의 local gradient이므로

 

z에 대한 gradient와 local gradient의 곱으로 표현 할 수 있다.

 

이것을 통해 상위 노드 방향으로 출력 gradient와 local gradient의 곱으로

 

입력에 대한 gradient를 계산할 수 있다는 것을 알 수 있다.

 

이처럼 각 노드가 local gradient를 갖고 있으며,

 

backpropagation을 통해 상위 노드 방향으로 계속 전달되고

 

이것을 전달받아 local gradient와 곱하기만 하면 되는 것이다.

 

하지만 실제 입력값들은 scalar가 아닌 vector로 구성되어 있다.

 

그래서 backpropagation을 vectorized operation을 통해 수행해야한다.

 

mini-batch 크기의 jacobian matrix를 계산하게 되는데

 

이 부분은 생략하기로 한다. (...)

 

이제 신경망(neural network)에 대해 살펴보자.

 

 

위의 2-layer NN을 보면

 

처음에는 선형 layer인 w와 x의 행렬 곱이고

 

이를 비선형성 함수인 max(0, w)를 이용하여 max를 얻는다.

 

그리고 여기에 선형 layer인 행렬 곱을 통해

 

최종적으로 score 함수를 얻을 수 있다.

 

여기서 비선형 변환이 중요하다.

 

이 비선형 변환이 없이 선형 함수만 추가된다면

 

f(f(f(x))) 이런식이 되어버린다.

 

이 결과는 다시 입력의 선형 함수가 되어버린다.

 

이렇게 되면 layer를 쌓을 수 없게 된다. 선형 함수를 쌓아봤자 선형적인 함수가 되버린다.

 

비선형의 복잡한 함수를 만들기 위해 간단한 함수들을 계층적으로 여러개 쌓아올린다.

 

기존에 선형 layer 행렬곱에 의한 score 함수를 보자. f=Wx

 

가중치 행렬 w의 각 행이 클래스 각각의 템플릿과 비슷한지 비교하였다.

 

W1을 하단 이미지로 표현한거라고 생각하자.

 

여기에서 문제는 각 클래스 마다 오직 하나의 템플릿만 가지고 있다는 것이다.

 

예를 들어, 자동차는 색상이 다양할 수 있지만 위의 자동차 템플릿은 빨간색을 주로 찾는거로 보인다.

 

또한 자동차가 트럭일수도 있고 여러 종류가 될 수 있지만 위의 템플릿은 스포츠가 느낌이 난다.

 

우리는 다양한 형태의 자동차를 분류하기를 원한다.

 

multi layer network는 이러한 것을 가능하게 한다. (W2 추가)

 

다른 비선형 행렬 w3로 곱하면 3-layer NN이 된다.

 

물론 중간에 비선형 함수 max를 거친다.

 

이런식으로 layer를 쌓으면서 deep neural network라는 용어가 생겼다.

 

왼쪽 위의 그림은 뉴런의 다이어그램을 나타낸다.

 

각 뉴런은 수상돌기(dendrite)를 지니고 있다.

 

수상돌기는 뉴런에서 들어오는 신호를 받는다.

 

세포체(cell body)는 들어오는 신호를 종합한다.

 

합쳐진 모든 신호는 하류 뉴런과 연결된 다른 세포체로 축삭(axon)을 통해 이동된다.

 

이는 위에서 살펴봤던 computational node가 실제 뉴런과 비슷하게 동작한다는것을 알 수 있다.

 

오른쪽 하단 그림을 보면

 

computational graph에서 노드가 서로 연결되어 있고

 

입력되는 신호는 x이다.

 

모든 x(x0, x1, x2)는 가중치 w와 결합되어 합쳐진다.

 

그리고 활성 함수를 적용하여 출력값을 얻으며 아래로 연결된 뉴런에게 전달된다.

 

왼쪽 하단의 그림은 활성화 함수 sigmoid이다.

 

위의 그림은 FC(fully-connected) layer로 구성된 신경망이다.

 

각 layer는 행렬곱을 했고, 2-layer NN은 선형 layer를 2개 가지고 있는 것을 의미한다.

 

이것을 하나의 hidden layer network라고 나타낼 수 있다.

 

행렬 곱의 수를 세는 대신 히든 레이어의 수를 센다.

 

그래서 2 layer NN을 1 hidden layer NN이라고 부를 수 있다.

 

마찬가지로 3 layer NN을 2 hidden layer NN이라고 부를 수 있다.

 

위의 그림에 f는 sigmoid 함수이다.

 

데이터를 x로 받고, 가중치 w1과 행렬곱을 한다.

 

그리고 sigmoid 함수를 통해 비선형성을 적용하고 h1을 얻는다.

 

그 다음 두 번째 hidden layer인 h2를 얻기 위해

 

h1과 w2를 행렬곱을 한다.

 

그리고 비선형성을 적용시키고 w3와 행렬곱을 함으로써 최종 출력을 얻는다.

위의 그림은 3개의 학습 데이터에 대해 임의의 가중치 W 행렬을 가지고 예측한 10개의 클래스 스코어이다.

 

굵게 표시된 스코어를 보면 이 보다 스코어가 더 높은 것도, 낮은 것도 볼 수 있다.

 

예를 들어 고양이 이미지에서 고양이 클래스의 스코어가 가장 높기를 기대하지만

 

예측된 점수는 2.9로 그리 높지 않으며 개구리가 3.78로 더 높다.

 

이 스코어를 보면 이 분류기는 그리 좋지 않다.

 

우리는 정답 클래스, 여기서는 고양이가 가장 높은 점수를 예측하는 분류기를 원한다.

 

동일한 가중치 W를 가지고 다른 이미지를 보자.

 

자동차 이미지에서는 자동차 점수가 6.04 가장 높다.

 

자동차에 대한 분류 성능이 괜찮은 가중치 W라고 볼 수 있다.

 

개구리 이미지에서 개구리 점수는 -4.34로 다른 점수들보다 훨씬 낮다.

 

이렇게 스코어를 확인하고 분석하는 방법은 좋지 않다.

 

어떤 알고리즘을 만들고 어떤 가중치 W가 가장 좋은지, 나쁜지를 결정하기 위해서는

 

가중치 W가 좋은지 나쁜지에 대해 정량화할 방법이 필요하다.

 

가중치 W를 입력으로 받아 각 스코어를 확인하고,

 

이 가중치 W가 얼마나 좋은지 나쁜지를 정량적으로 측정하는 것이 바로 손실함수(Loss Function)이다.

 

그리고 가중치 행렬 W가 될 수 있는 모든 경우의 수에 대해서

 

'가장 덜 나쁜' W가 무엇인지를 찾아야 한다.

 

이 과정이 최적화(Optimization)이다.

 

여기서는 3개의 트레이닝 이미지와 3개의 클래스를 사용한다. 10개는 너무 많으니까.

 

점수를 보면 고양이는 잘 분류하지 못했고, 자동차는 잘 분류했고, 개구리는 점수가 최악이다.

 

이를 손실함수로 공식화해보자.

 

트레이닝 데이터 x가 있다. x는 알고리즘의 입력으로 image classification 문제라면 이미지가 될 것이다.

 

레이블 데이터 y가 있다. y는 image classification 문제라면 해당 이미지에 대한 레이블이 될 것이다.

 

10개의 클래스라면 레이블 y는 1에서 10사이의 정수값이 된다. 프로그래밍 언어에 따라 0~9일수도 있다.

 

어째든 y라는 정수값은 입력 이미지 X에 대한 정답 카테고리를 의미한다.

 

앞서 예측함수 f를 정의했다.

 

입력 이미지 x와 가중치 행렬 w를 입력으로 받아서 새로운 테스트 이미지에 대해 y를 예측하는 것이다.

 

위에 말한대로 cifar-10의 경우 y는 10개가 된다.

 

손실함수 Li를 정의해보자.

 

Li는 예측함수 f와 정답값 y를 입력으로 받아 트레이닝 샘플을 얼마나 예측하는지 정량화한다.

 

최종 loss인 L은 데이터셋에서 각 N개의 샘플들의 loss의 평균이 된다.

 

이러한 L 함수는 image classification 문제에 국한되지 않는 아주 일반적인 공식이다.

 

좀 더 나아가 다른 딥러닝 알고리즘을 살펴보자면, 어떤 알고리즘이던 가장 일반적으로 진행되는 일은,

 

어떤 x와 y가 존재하고, 가중치 w가 얼마나 좋을지를 정량화하는 손실 함수를 만드는 것이다.

 

구체적으로 한 손실 함수를 살펴보자. 이 손실 함수는 image classification에 아주 적합하기도 하다.

 

바로 multi-class SVM loss이다.

 

이 loss는 힌지 로스(hinge loss)라고도 불린다.

 

위에 언급한 기본적인 loss와 비슷하지만 조건이 생겼다.

 

sj는 '정답이 아닌' 클래스의 스코어이다.

 

syi는 '정답' 클래스의 스코어이다.

 

조건을 보면 if 정답 클래스 스코어(syi)가 정답이 아닌 클래스 스코어(sj) + safety margin(여기서는 1) 값보다 

 

크거나 같으면 loss가 0이 된다.

 

그리고 위의 조건이 아니면(otherwise),

 

정답이 아닌 클래스 스코어(sj) - 정답 클래스 스코어(syi) + safety margin(여기서는 1) 값을 loss로 한다.

 

만약 정답인 클래스 스코어가 정답이 아닌 클래스 스코어 + safety margin(여기서는 1)보다 크면 loss가 0이 되며,

 

loss가 0이라는 것은 매우 좋다는 것이다.

 

syi가 sj보다 충분히 커야 잘 분류했다고 할 수 있다.

 

그런데 근소한 차이로 분류한다면 새로운 테스트 이미지에서 틀릴 경우가 생길 것이다.

 

safety margin을 포함해서 더 큰 차이로 분류했을때를 Loss가 0인 경우로 정의한다.

 

그래프로 그리면 위와 같은 그림이 된다.

 

이 모양이 경첩처럼 생겼다고 해서 hinge loss라고 이름이 붙여졌다.

 

다음 예시를 보자.

 

SVM loss는 앞서 조건들에 의해 오른쪽 파란색 박스와 같이 정의된다.

 

고양이 클래스를 보자.

 

우선 정답이 아닌 클래스(자동차)의 점수(sj)를 살펴보면,

 

자동차 점수가 5.1, 고양이 점수가 3.2로 자동차가 높다.

 

5.1 - 3.2 + 1 = 2.9가 된다.

 

또 다른 정답이 아닌 클래스(개구리)의 점수(sj)를 살펴보면,

 

개구리 점수가 -1.7, 고양이 점수가 3.2로 고양이가 높다.

 

-1.7 - 3.2 + 1 = -3.9

 

이는 0 보다 작으므로 loss는 0이 된다.

 

이들의 합(시그마)을 구해야하기 때문에 더해준다.

 

2.9 + 0 = 2.9 가 고양이 클래스의 loss가 된다.

 

자동차 클래스와 개구리 클래스에도 동일하게 적용해보자.

 

자동차 클래스는 명확합니다.

 

왜냐하면 자동차가 아닌 클래스(고양이, 개구리) 둘 다 + 1(safety margine)을 해도

 

자동차 스코어를 넘지 못하기 때문이다. 그럼 loss가 전부 0이 나온다.

 

개구리 클래스를 보자.

 

개구리 loss를 구하니까 12.9가 나온다. 고양이 클래스는 2.9 였는데 개구리는 12.9가 나온다.

 

고양이 클래스에서 고양이 점수가 개구리보단 점수가 높았기 때문에 loss가 비교적 낮은것이다.

 

개구리를 분류하는 것에 있어서 12.9만큼 안좋다는 의미이며, 고양이 분류보다 훨씬 안좋다고 볼 수 있다.

 

최종적으로 loss를 다 더하고 (2.9 + 0 + 12.9) 클래스가 3개니 3으로 나눠서 평균을 구한다.

 

그렇게 계산된 5.27이 최종 loss가 된다.

 

만약 자동차의 점수를 살짝만 바꾸면 어떻게 될까?

 

예를 들어 자동차 클래스에서 자동차 점수가 -1이 되어서 3.9가 됐다고 가정해보자.

 

그래도 loss는 0으로 변함없을 것이다.

 

왜냐하면 고양이(1.3)에 1을 더해도 개구리(2.0)에 1을 더해도 자동차가 더 높기 때문이다.

 

여기서 SVM hinge loss의 특성을 알 수 있다.

 

데이터에 민감하지 않다는 것이다. 점수가 몇 점인지는 관심이 없다.

 

단지 정답 클래스의 점수가 정답이 아닌 클래스의 점수보다 높은가에만 포커스를 두고 있다.

 

두번째 질문으로 loss 최소/최대는 무엇일까?

 

loss의 최소는 0이 된다. 0 보다 작으면 0이 max값으로 loss가 되기 때문이다.

 

최대값은 무한대가 된다.

 

만약 초기 W가 매우 작아서 스코어가 0에 가까워지면 loss는 어떻게 될까?

 

스코어가 0에 가까워지면 safety margin(여기서는 1)만 남을거고

 

각 로스는 1+1=2가 될 것이다. 3개의 클래스니 (2+2+2) / 3 = 2가 나온다.

 

클래스가 10개라면 (9+9+9... ) / 10 = 9가 될 것이다.

 

결국 로스는 클래스 개수 - 1이 된다.

 

이건 디버그 용도로 많이 사용된다.

 

가중치 W를 0으로 해주면 loss가 클래스 개수 - 1이 잘 나오는지 검사해보는 것이다.

 

이걸 sanity check라고도 부른다.

 

4번째 질문으로 지금까지 우리는 정답 클래스의 점수는 제외시켜 loss를 계산했는데, 왜 제외시킬까?

 

만약 정답 클래스 점수를 포함해서 계산하면 어떻게 될까?

 

고양이 클래스에서 3.2 - 3.2 + 1 = 1 이렇게 되고, 자동차, 개구리 또한 마찬가지이다.

 

그럼 평균이 1 증가하는 효과와 마찬가지가 된다.

 

우리는 최종 loss가 0이 되길 바란다. 하지만 이렇게 되면 1이 제일 좋은 loss가 된다.

 

5번째 질문으로 만약 sum대신 mean을 사용하면 어떻게 될까?

 

로스를 더해서 해당 클래스의 loss라고 정의하는 것 대신

 

평균을 낸다면 loss의 스케일만 작아질 뿐이다. 때문에 별차이 없게 된다.

 

만약 제곱을 하면 어떻게 될까?

 

이때는 loss가 다르게 된다. 일단 제곱을 하게 되면 non-linear하게 된다.

 

제곱을 해서 구하는 방법을 squared hinge loss라고 한다.

 

때에 따라 잘 동작될 수 있다.

 

왜냐하면 hinge loss 그래프에서 직선이 아닌 곡선(제곱승)으로 올라가기 때문이다.

 

그래서 '매우 매우 안좋다' 혹은 '매우 매우 좋다'를 볼때 유용할 수 있다.

 

하지만 일반적으로는 제곱을 사용하지 않는다.

 

여기에 또 하나의 문제가 있다.

 

우리가 최적의 가중치 W를 찾았다고 하면 이 W는 unique한 값일까?

 

정답은 아니다.

 

가중치에 2배를 해도 역시 loss는 0을 갖게 된다.

 

가중치에 2배를 직접 계산을 하면 위의 그림과 같다.

 

마찬가지로 loss가 0이 되는것을 볼 수 있다.

 

즉, W는 여러개가 될 수도 있다는 점이다.

 

W가 여러개 있을 수 있는것이 어떻게 문제가 될까?

 

우리는 train 보다 test에 관심이 더 크다. 새로운 값에 대해 '예측'하고 싶은 것이다.

 

하지만 여지껏 가중치 w는 트레이닝셋에 맞추게 진행했다.

 

그래서 가중치 W는 트레이닝셋에 맞춰졌다.

 

이 가중치 W가 테스트셋에도 맞춰져 있을까? 아니다.

 

W는 unique하지 않기 때문에 테스트셋에는 해당 W가 안좋을수 있다.

 

위의 그림을 보면 파란색 선으로 W를 구했다고 가정하자.

 

새로운 초록색 샘플이 들어왔을때 잘 예측할 수 있을까? 그렇지 못하고 정확도가 낮을 것이다.

 

이를 과적합(overfitting)이라고 한다.

 

파란색 선보다 초록색 선이 낫다는 것이다.

 

즉, 테스트셋에도 알맞은 W를 찾아야한다.

 

그래서 수식의 오른쪽에 regularization 텀이 온다.

 

data loss는 트레이닝 입장에 있고 regularization은 테스트 입장에 있다.

 

만약 트레인셋에만 맞는 가중치 W를 학습하려고 할때 regulaization은 어느정도 패널티를 부여한다.

 

입력이 복잡하기 때문에 가중치 W도 고차원으로 학습하려는 경향이 있다.

 

이에 대해 패널티를 부과하는 것이다.

 

occam's razor는 과학계에서 사용하는 말이다.

 

어떤 가설이 세울때 단순한게 더 좋다는 의미를 가진다.

 

L1 regularization을 살펴보자.

 

loss function에 해당하는 부분은 기존 loss를 나타낸다.

 

때문에 기존 loss에 가중치의 절대값만큼의 패널티를 달아주는것과 같다.

 

이는 cost를 더 커지게 만들어서 가중치 w를 과도한 변화를 막는다고 볼 수 있다.

 

이상치에 대한 W를 0으로 만들어버리는 특징이 있다.

 

여기서 람다는 regularization strength로 하이퍼파라미터이다.

 

이것이 작아질수록 약한 정규화가 된다.

 

이렇게 L1 regularization을 사용하는 선형 회귀 모델을 Lasso model이라고도 한다.

 

L2 regularization을 살펴보자.

 

마찬가지로 기존 loss에 regularization 텀이 붙는 형태이다.

 

다른 점은 가중치의 제곱을 더해주는 것이다.

 

이상치에 대한 W를 0으로 만들지는 않고 0에 가깝게 만든다.

 

때문에 L1에 비해 L2가 generalization 을 항상 개선시킬 수 있는 것으로 알려져있다.

 

L2 regulaization을 사용하는 선형 회귀 모델을 Ridge model이라고도 한다.

 

multiclass SVM loss 외에도 딥러닝에서 자주 쓰이는 softmax가 있다.

 

multinomial logistic regression이라고도 불린다.

 

딥러닝에서는 이걸 훨씬 많이 쓴다.

 

multiclass SVM loss에서는 스코어 자체에 대한 해석은 고려하지 않았다.

 

스코어 자체는 크게 신경안썼고 safety magin을 포함해서 높은지 낮은지만 판단했다.

 

하지만 multinomial logistic regression의 손실함수 softmax function은 스코어 자체에 추가적인 의미를 부여한다.

 

빨간 네모 박스 수식을 이용하여 스코어를 가지고 클래스 별 확률 분포를 계산한다.

 

in summary 수식을 살펴보면,

 

(분모) 모든 스코어에 exp를 취하고 그걸 다 더한 다음

 

(분자) 원하는 클래스의 점수를 exp 취해서 나눈다.

 

이렇게 되면 '확률' 값이 된다.

 

예를 들어 1 / 1 + 2 를 하면 1의 확률은 1/3이 된다.

 

그리고 이걸 -log를 취해서 loss를 계산한다.

 

그럼 왜 exp와 -log를 붙일까?

 

softmax는 multinomial logistic regression이다.

 

logistic regression은 sigmoid function으로도 불린다.

 

sigmoid function은 위의 그림에서 왼쪽 그래프에 해당된다.

 

수식을 보면 exp가 취해져있다. 그렇기 때문에 exp를 사용한다.

 

-log를 취하는 이유는 오른쪽 그림과 같다.

 

우리는 '얼마나 안좋을지'에 대해 판단해야한다.

 

x축이 확률, y축이 loss라고 생각하면,

 

-log가 확률이 1에 가까워질수록 loss가 0에 가까워진다.

 

즉, x축(확률)에서 우리가 원하는 클래스의 정답률이 1에 가까워질수록 y축(loss)은 0에 가까워진다.

 

때문에 -log를 사용한다.

 

직접 계산을 해보자.

 

아까의 점수에 exp를 취하면 위와 같은 값이 나온다.

 

그리고 전체를 더한 값 188.68을 각각 나눠준다.

 

그러면 24.5는 24.5 / 188.68로 0.13이 나오게된다.

 

마지막으로 원하는 정답 클래스에 -log를 취해준다.

 

-log(0.13)은 0.89이며, 0.89만큼 안좋다라고 평가할 수 있다.

 

지금까지 내용을 정리해보자.

 

우리에세 데이터셋 x와 y가 있다.

 

입력 x로부터 스코어를 얻기위해 linear classifier를 사용한다.

 

softmax, svm loss와 같은 손실함수를 이용해서

 

모델의 예측 값이 정답에 비해 얼마나 별로인지 측정한다.

 

그리고 모델의 '복잡함'과 '단순함'을 통제하기 위해 손실 함수 regularization term을 추가한다.

 

지금까지 우리가 supervised learning이라고 부르는 것에 대한 전반적인 개요를 알아보았다.

 

우리가 딥러닝에서 배울 내용은

 

어떤 복잡한 함수 f를 정의하고, 그 가중치 값이 주어졌을때

 

알고리즘이 얼마나 안좋게 동작하는지 측정하는 손실 함수를 작성하는 것이다.

 

그리고 모델이 복잡해지는것을 어떻게 막을지에 대한 regularization term을 추가한다.

 

이 모든걸 합쳐서 최종 손실 함수가 최소가 되게 하는 가중치 행렬 W를 구하는 것이다.

 

그렇다면 실제로 어떻게해야 하는 것일까?

 

어떻게하면 실제 loss를 줄일 수 있는 w를 찾을 수 있을까?

 

최적화(optimization)는 우리가 엄청 큰 계곡을 걷고 있는 것과 같다.

 

다양한 산과 계곡과 시내가 있는 엄청 큰 골짜기를 거닐고 있는 것이다.

 

그리고 '산'과 '계곡'과 같은 풍경들이 loss라고 보면 된다.

 

우리가 이 골짜기를 돌아다니는 한 사람이고

 

있는 곳의 '높이'가 바로 loss이다.

 

loss는 w에 따라 변하게 되고, 우리는 w를 찾아야 한다.

 

어떻게든 이 골짜기의 밑바닥을 찾아내야한다.

 

하지만 일반적으로 이런 문제들은 매우 어렵다.

 

그렇기 때문에 반복적인 방법 iterative한 방법을 사용한다.

 

이 방법들은 임의의 지점에서 시작해서 점차적으로 성능을 향상시키는 방법이다.

 

가장 먼저 생각해볼 수 있는 단순한 방법은 임의 탐색(random search)이다.

 

임의로 샘플링한 W들을 많이 모아놓고 loss를 계산해서 어떤 W가 좋은지 살펴보는 것이다.

 

이 방법은 절대 사용하면 안된다.

 

하번쯤은 '상상'해볼만한 방법이긴하다.

 

위의 그림처럼 실제로 해볼수도 있으며, linear classifier를 학습시킬 수 있다.

 

cifar-10에서 클래스가 10개이니 임의의 확률은 10%가 되고,

 

무작위 시행을 거치면 어떤 W를 구해볼 수 있는데 이 예시에서는 약 15% 정확도를 보여준다.

 

10개중 하나를 찍는 것보다 좀 더 나은 수준이다.

 

SOTA는 95% 정확도를 가진다 (2017년인걸 감안, 현재는 더 높다)

 

더 나은 전략은 지역적 기하학 특성(local geometry)을 이용하는 것이다. 

 

위의 그림과 같이 서있다면 어느 방향으로 가야 내려갈 수 있을까?

 

두 발로 땅의 경사를 느끼고, 어느 방향으로 내려가야할지 느낄 수 있다.

 

그 방향으로 한발자국 내딛고, 다시 두 발로 느끼는 방향을 다시 찾는다.

 

이렇게 반복하다보면 결국 골짜기를 다 내려갈 수 있다.

 

그렇다면 경사(slope)는 무엇일까?

 

1차원 공간에서 slope는 어떤 함수에 대한 미분값이다.

 

1차원 함수 f(x) = y 가 있다고 가정하자. 

 

x를 입력으로 받으면 출력은 어떤 커브의 높이라고 할 수 있다.

 

곡선의 일부를 구하면 기울기를 계산할 수 있다.

 

어떤 점(x)에서의 경사, 즉 도함수(derivative)를 계산해보면

 

작은 스텝 h가 있고, 이 스텝 간의 함수 값의 차이를 비교해 보면

 

f(x+h) - f(x)가 된다.

 

그리고 이 스텝 사이즈를 0으로 만들면 (h->0)

 

이것이 바로 어떤 점에서 이 함수의 경사가 된다.

 

그리고 이 수식을 다변수 함수(multi-variable function)로 확장시킬 수 있다.

 

실제 x는 스칼라 값이 아닌 벡터 값이 된다.

 

x가 벡터이기 때문에 위의 개념을 다변수로 확장시켜야 한다.

 

다변수 상황에서 미분으로 일반화를 해보면 gradient가 되고,

 

gradient는 벡터 x의 각 요소에 대한 편도함수들의 집합이다.

 

gradient 모양은 x와 같다. x가 3개면 gradient도 3개.

 

그리고 gradient의 각 요소가 알려주는 것은 '우리가 그쪽으로 갈때 함수 f의 경사가 어떤지' 이다.

 

gradient를 이런 유용한 정보를 얻을 수 있다. gradient는 편도함수들의 벡터이다.

 

gradient의 방향은 함수에서 '가장 많이 올라가는 방향' 이 된다.

 

반대로는 '가장 많이 내려갈 수 있는 방향'이 된다.

 

그렇다면 특정 방향에서 얼마나 가파른지 알고 싶으면 어떻게 해야 할까?

 

해당 방향의 단위 벡터(unit vector)와 gradient 벡터를 내적하면 된다.

 

gradient는 매우 중요하다. 왜냐하면 gradient가 함수의 어떤 점에서 선형 1차 근사 함수를 알려주기 때문이다.

 

그래서 실제로 많은 딥러닝 알고리즘들이 gradient를 계산하고,

 

가중치 W를 반복적으로 업데이트할때 gradient를 사용한다.

 

컴퓨터로 이 gradient를 써먹을 수 있는 가장 단순한 방법 중 하나는,

 

유한 차분법(finite difference method)를 이용하는 것이다.

 

왼쪽에 가중치(파라미터) 벡터 W가 있다.

 

이 W를 사용하면 1.25347 loss를 가진다.

 

여기서 우리는 gradient 'dW'를 구해야 한다.

 

gradient의 각 요소가 말해주는 것은 우리가 한 방향으로 아주 조금 이동했을때

 

loss가 어떻게 변하는지에 대한 것이다.

 

일단 W가 있고, W의 첫번째 요소 0.34에 아주 작은 값 h, 0.0001을 더해보는 것이다.

 

그리고 다시 loss를 계산한다.

 

loss가 1.25322로 기존의 1.25347보다 loss가 줄은 것을 볼 수 있다.

 

이는 첫 번째 요소를 조금 움직이면 loss가 감소한다는 사실을 알 수 있다.

 

이제 극한 식을 이용해서 유한 차분법으로 근사시킨 gradient를 구한다.

 

첫번째 요소의 gradient는 -2.5이다.

 

이제 첫 번째 요소의 값은 원래대로 돌려놓고

 

두번째 요소를 h 만큼 증가시킨다.

 

그리고 다시 loss를 계산하고 유한 차분법을 이용해서

 

두번째 요소의 gradient의 근사치를 계산할 수 있다.

 

이렇게 계속 반복합니다.

 

이는 시간이 엄청 오래걸리는 방법이다.

 

이 함수 f가 CNN과 같이 엄청 큰 함수였다면, 훨씬 더 오래 걸릴 것이다.

 

여기서는 파라미터 W가 10개뿐이 없지만

 

크고 깊은 신경망에서는 파라미터가 수천, 수억개일 수 있다.

 

그렇기 때문에 실제로는 이런식으로 gradient를 계산하지 않는다.

 

왜냐하면 gradient 하나를 계산하기 위해 수천개의 함수값을 일일이 다 계산해야하기 때문이다.

 

위의 두 인물(아이작 뉴턴, 라이프니츠) 덕분에 손실 함수를 적어놓고 '미분'이라는 마법의 망치를 두드리면

 

gradient가 계산되서 나온다.

 

해석적(analytic)으로 계산하는 것이 수치적으로 계산하는 것보다 더 효율적이다.

 

더 정확하기도 할 뿐더러, 식 하나로 계산할 수 있기 때문에 훨씬 더 빠르다.

 

W의 모든 원소를 순회하면서 gradient를 계산하는것이 아니라,

 

gradient를 나타내는 식이 무엇인지 찾고

 

그걸 수식으로 나타내서 한번에 gradient dW를 계산하는 것이다.

 

위의 세 줄의 간단한 알고리즘은

 

크고 복잡한 신경망 알고리즘을 어떻게 학습시킬것인가에 대한

 

핵심 아이디어를 지니고 있다.

 

gradient descent는 우선 w를 임의의 값으로 초기화한다.

 

그리고 loss와 gradient를 계산하고,

 

가중치를 gradient 반대 방향으로 업데이트한다.

 

gradient가 함수에서 증가하는 방향이기 때문에

 

-gradient를 해야 반대방향으로 내려가는 방향이 된다.

 

그럼 -gradient 방향으로 조금씩 이동할 것이고

 

이걸 계속 반복하다보면 결국 수렴할 것이다.

 

하지만 스텝 사이즈는 하이퍼파라미터이다.

 

스텝 사이즈는 -gradient 방향으로 얼마나 나아가야하는지 알려준다.

 

스텝 사이즈를 학습률(learning rate)이라고도 하며,

 

실제 학습시 정해줘야하는 가장 중요한 하이퍼파라미터중 하나이다.

 

위의 그림은 2차원 공간에서의 gradient descent 예시이다.

 

하얀색 원이 손실함수이다.

 

가운데 빨간 부분이 낮은 loss이고 파란색으로 갈수록 높은 loss를 나타낸다.

 

임의의 점 W를 설정하고 -gradient를 계산해서

 

loss가 낮은 지점에 도달할 것이다.

 

이걸 계속 반복하게 되면 결국은 최저점에 도달할 수 있을 것이다.

 

손실 함수 정의를 생각해보면

 

loss는 각 트레이닝 샘플을 분류기가 얼마나 '안좋게' 분류하는지를 계산하는것이고,

 

전체 loss는 전체 트레이닝셋 loss합의 평균을 사용했다.

 

하지만 실제로는 N(트레이닝 샘플)이 엄청 커질 수 있다.

 

ImageNet 데이터셋의 경우 N은 130만개이다.

 

따라서 loss를 계산하는것은 매울 오래걸리는 작업이 된다.

 

수백만번의 계산이 필요할 수 있으며, 이는 매우 느릴 수 있다.

 

gradient는 선형 연산자이기 때문에

 

실제 gradient를 계산하는 과정을 보면,

 

loss는 각 데이터 loss의 gradient 합계라는 것을 알 수 있다.

 

그렇기 때문에 gradient를 한번 더 계산하려면,

 

N개의 전체 데이터셋을 한번 더 돌면서 계산해야한다.

 

N이 130만이면 엄청 느릴수밖에 없다.

 

W가 업데이트 되려면 엄청 많은 시간을 기다려야할 것이다.

 

그래서 실제로는 stochastic gradient descent 방법을 쓴다.

 

전제 데이터셋의 gradient와 loss를 계산하는것이 아니라

 

mini-batch라는 작은 트레이닝 샘플 집합으로 나눠 학습을 진행한다.

 

mini-batch는 보통 2의 승수로 정하며, 보통 32, 64, 128을 사용한다.

 

작은 mini-batch를 이용해서

 

loss의 전체 합의 '추정치'와

 

실제 gradient의 '추정치'를 계산한다.

 

그래서 stochastic 하다는 것은 Monte Carlo Method의 실제 값 추정 방법과 유사하다고 볼 수 있다.

 

코드가 4줄로 늘었다.

 

임의의 mini-batch를 만들어내고 mini-batch에서 loss와 gradient를 계산한다.

 

그리고 W를 업데이트한다.

 

loss의 '추정치'와 gradient의 '추정치'를 사용하는 것이다.

 

SGD는 거의 모든 Deep NN알고리즘에 사용되는 기본적인 학습 알고리즘이다.

 

이제 이미지 특징(feature)에 대해 살펴보자.

 

linear classifier는 실제 raw image 픽셀을 입력으로 했다.

 

하지만 이런 방법은 좋은 방법이 아니다.

 

multimodality와 같은 이유 때문이다. (말 머리 두개)

 

영상 자체를 입력으로 사용하는 것은 성능이 좋지 않다. (hand crafted feature 관점에서)

 

그래서 DNN이 유행하기 전에 주로 쓰는 방법은 2 stage를 거치는 것이였다.

 

첫번째는 이미지가 있으면 여러가지 특징 표현을 계산하는 것이다.

 

이런 특징 표현은 이미지의 모양새와 관련된 것일 수 있다.

 

그리고 여러 특징 표현들을 연결(concat)시켜 하나의 특징 벡터로 만든다.

 

이러한 특징 벡터가 linear classifier의 입력으로 들어가는 것이다.

 

위의 그림과 같이 트레이닝셋이 있다고 가정하자.

 

빨간점들이 가운데 있고 주변에 파란점들이 있다.

 

이 데이터셋에서 linear한 결정 경계를 그릴 방법이 없다.

 

하지만 적절한 특징 변환을 거친다면,

 

복잡한 데이터가 변환 후 선형으로 분리 가능하게 바뀔 수 있다.

 

이런 방법은 문제를 풀 수 있도록 하려면 어떤 특징 변환이 필요한가를 알아내는 것들이다.

 

이미지의 경우 픽셀을 극좌표계로 바꾸는것이 말이 안되지만

 

극좌표계로 바꾸는것을 일종의 특징 변환이라고 생각한다면 이해될 수 있다.

 

실제로 분류기에 raw 픽셀값을 넣는것보다 성능이 더 좋을수도 있다.

 

특징 변환의 예로 컬러 히스토그램이 있다.

 

이미지의 hue 값만 뽑아서 모든 픽셀을 카운팅하는것이다.

 

해당하는 색상의 픽셀 개수를 세는 것이다.

 

이는 이미지가 전체적으로 어떤 색인지 알려준다.

 

위의 개구리를 보면 초록색 계열이 많은 것을 볼 수 있다. 자주색이나 붉은색은 별로 없다.

 

실제로 사용하는 간단한 특징 벡터라고 볼 수 있다.

 

NN이 뜨기 전에 인기있었던 특징 벡터 중 하나는 histogram of oriented gradients(HOG)이다.

 

local orientation edges를 측정한다.

 

이미지를 8x8 픽셀로 나누고, 이 지역 내에서 가장 영향력있는 edge의 방향을 계산한다.

 

그리고 이를 양자화해서 histogram을 만든다.

 

다양한 edge orientation에 대한 히스토그램을 계산하는 것이다.

 

그러면 전체 특징 벡터는

 

각각의 모든 8x8 지역들이 가진 edge orientation에 대한 히스토그램이 되는 것이다.

 

위의 개구리를 보면 이파리 위에 앉아있는 것을 볼 수 있다.

 

이파리들은 주로 대각선 edge를 가지고 있다.

 

HoG로 시각화해 보면 이파리 부분에 많은 대각 edge가 있다는 것을 알 수 있다.

 

이는 HoG의 특징 표현이라고 볼 수 있다.

 

HoG는 영상 인식에서 정말 많이 활용한 특징 벡터이다.

 

또 하나의 특징 표현은 Bag of Words(BOW)이다.

 

이 아이디어는 자연어처리(NLP)에서 영감을 받은 것이다.

 

어떤 문장이 있고 BOW에서 이 문장을 표현하는 방법은 

 

문장의 여러 단어의 발생 빈도를 세서 특징 벡터로 사용하는 것이였다.

 

이와 같은 직관을 이미지에 적용한 것이 BOW이다.

 

우선 시각 단어(visual words)라고 하는 용어를 정의했으며,

 

2단계의 과정을 거친다.

 

엄청 많은 이미지를 이용해서 그 이미지들을 임의로 조각낸다.

 

그리고 그 조각들을 k-means와 같은 알고리즘으로 군집화한다.

 

이미지내의 다양한 것들을 표현할 수 있는 다양한 군집들을 만들어내는 것이다.

 

위의 그림에서 오른쪽을 보면, (step 1)

 

이는 이미지들에서 다양한 이미지 패치를 뽑아서 군집화 시켜 높은 예이다.

 

군집화 단계를 거치면 시각 단어는 빨간색, 노란색, 파랑색과 같은 다양한 색을 포착할 수 있다.

 

또한 다양한 방향의 oriented edge들도 포착할 수 있다.

 

이 방법은 edge들을 데이터 중심적인 방법을 통해 얻어냈다는 점에서 매우 흥미롭다.

 

이런 시각 단어 집합인 'codebook'을 만든 다음,

 

어떤 이미지가 있으면 이 이미지에서 시각 단어들의 발생 빈도를 통해

 

이미지를 인코딩 할 수 있다.

 

이는 이 이미지가 어떻게 생겼는지에 대한 다양한 정보를 제공한다.

 

Image classification의 pipe line은 위의 그림과 같다.

 

5~10년 전까지만 해도 이미지를 입력받으면

 

BOW나 HOG와 같은 다양한 특징 표현을 계산하고,

 

계산된 특징들을 모아 연결해서 만든 벡터를 linear classifier의 입력으로 사용했다.

 

특징이 한번 추출되면 feature extractor는 분류기를 학습하는동안 업데이트하지 않는다.

 

학습중에는 오직 linear classifier만 학습이 된다.

 

DNN을 보면 크게 다르진 않지만

 

이미 만들어 놓은 특징들을 사용하는것이 아닌

 

데이터로부터 특징들을 직접 학습하려한다는 점이 다른점이다.

 

그렇기 때문에 raw 픽셀이 cnn에 그대로 입력되고

 

여러 레이어를 거쳐서 데이터를 통한 특징 표현을 직접 만들어내게 된다.

 

따라서 linear classifier만 훈련하는게 아니라 

 

가중치 W 전체를 한번에 학습한다.

 

 

우리가 Image classification을 수행한다고 생각해보자. 어떻게 해야 할까?

 

우선 이미지를 입력 받아야 할 것이다.

 

고양이 사진을 예로 들자.

 

우리 Image classification 시스템에는 미리 정해놓은 카레고리 집합이 존재한다.

 

개, 고양이, 자동차 등이 있을 수 있다.

 

이제 우리 알고리즘은 입력된 고양이 사진을 어떤 카테고리에 속할 지 정하는 일을 해야한다.

 

인간은 시각 인식 테스크에 고도화되어 있기에 매우 쉬워 보일수도 있지만

 

컴퓨터(기계) 입장에서는 매우 어려운 작업일 수 밖에 없다.

 

 

 

컴퓨터가 고양이 사진을 볼 때는 고양이라고 판단하지 못한다. 단지 해상도 크기의 숫자 집합으로 밖에 보이지 않는다.

 

거대한 숫자 집합에 불과하다.

 

각 픽셀은 red, green, blue 채널의 3개의 숫자로 표현된다. 

 

이 거대한 숫자 집합에서 '고양이' 라는 것을 인식하기는 상당히 어려운 일이다.

 

이러한 것을 '의미론적 차이(semantic gap)이라고 한다.

 

위 사진이 고양이라는 사실과 컴퓨터가 보는 픽셀 값과는 큰 차이가 있다.

 

 

 

고양이 사진에 작은 변화만 주더라도 픽셀 값들은 대부분 변하게 된다.

 

고양이를 촬영하는 카메라를 조금만 옆으로 옮겨도 모든 픽셀값들은 달라지게 된다.

 

하지만 달라진 픽셀 값에도 여전히 고양이라는 사실은 변하지 않는다.

 

우리가 만들려는 알고리즘은 이러한 변화에 강인해야 한다.

 

 

 

바라보는 방향 뿐만 아니라 외부 조명 또한 문제가 될 수 있다.

 

장면에 따라 조명이 천차만별로 달라지게 된다.

 

어두운 곳에든 밝은 곳이든 고양이라는 사실이 변하지 않는다.

 

이러한 조명 변화에도 강인한 알고리즘을 설계해야 한다.

 

 

 

고양이를 객체라고 표현하면 객체의 변형이 다양할 수 있다.

 

다양한 자세에도 불구하고 고양이는 고양이다.

 

이 또한 강인해야 한다.

 

 

 

가려지는 것도 문제가 될 수 있다. 사람은 고양이의 일부만 보아도 고양이라는 사실을 바로 알 수 있다.

 

가려져도 고양이는 고양이인 것이다.

 

우리의 알고리즘은 이러한 가림에도 강인해야 한다. 아주 어려운 문제일 수 있다.

 

 

 

고양이가 배경과 비슷해도 문제가 발생한다.

 

사람은 금방 눈치챌 수 있지만 기계는 그렇지 못하다.

 

이러한 문제도 다뤄야만 한다.

 

 

 

하나의 클래스 내에서도 다양성이 존재한다.

 

'고양이'라는 개념으로 모든 고양이의 다양한 모습들을 내포해야 한다.

 

고양이에 따라 다양한 생김새, 크기, 색, 나이 등이 전부 다르다.

 

알고리즘은 이러한 다양성도 강인해야 한다. 이러한 문제들은 매우 어렵다.

 

앞서 말한 여러 문제들을 전부 다룰 수 있는 알고리즘이며, 고양이뿐만 아니라 다양한 객체를 인식해야 한다면

 

이는 아주 어려운 문제일 것이다.

 

하지만 일부 제한된 상황을 가정한다며, 잘 동작할뿐만 아니라

 

수행 속도도 몇 ms 걸리지 않는 인간과 비슷한 수준의 알고리즘이 존재할 수 있다.

 

 

 

Image Classifier API 코드를 작성한다고 가정해보자.

 

위의 그림처럼 python 메서드를 작성해보지 않을까 싶다.

 

이미지를 입력받고 어떤 마법같은 일을 수행하면 해당 이미지의 알맞은 클래스를 반환하는 것이다.

 

하지만 이를 구현하기 위한 적절한 코드가 딱히 없을 것이다.

 

만약, 우리가 '숫자 정렬'이나 'convex hull 계산' 등의 문제를 풀어야 한다면,

 

우리는 알고리즘을 하나씩 작성하면서 필요한 모든 과정을 나열할 수 있을 것이다.

 

하지만 image classification의 경우, 그런 직관적이고 명시적인 알고리즘이 존재하지 않는다.

 

우리는 위의 함수를 만들려고 할때 이러한 문제를 맞이하게 된다.

 

 

 

기계학습이 등장하기 전에는 객체 인식을 하기위해 룰 기반의 코드를 만들어왔다.

 

예를들어 고양이는 두 개의 귀와 하나의 코가 있다는 것을 알고 있고,

 

Hubel과 Wiesel 연구에서 edge가 중요하다는 것도 알고 있다.

 

그렇다면 이미지의 edge를 계산하는것을 시도해볼만 하다.

 

그리고 다양한 corner와 edge들을 각 카테고리로 분류한다.

 

가령 세 개의 선이 만나는 점을 corner라고 했을 때, 귀는 여기에 corner 한개, 저기에 corner 한개 등등

 

이런식으로 고양이를 인식하기 위해 '명시적인 규칙 집합'을 써내려 가는 방법이다.

 

하지만 이러한 방법은 잘 동작하지 않는다.  이러한 알고리즘은 위에 나열했던 문제들에 강인하지 못하다.

 

또 다른 문제는 고양이가 아닌 강아지를 인식한다고 했을 때 또 다른 규칙에 대해 작성해야 한다.

 

다른 객체들에 대해서도 마찬가지로 재작성해야한다.

 

이러한 방법은 확장성이 전혀 없는 방법들이다.

 

이 세상에 존재하는 다양한 객체들에게 유연하게 적용할 수 있는 확장성이 있는 알고리즘을 만들어야 한다.

 

 

 

이러한 알고리즘을 가능하게 하는 하나의 insight는 '데이터 중심 접근방법(data-driven approach)이다.

 

고양이는 무엇이다, 강아지는 무엇이다, 자동차는 무엇이다, 이렇게 직접 어떤 규칙을 설계하는 것 대신에

 

인터넷에서 많은 양의 고양이, 강아지, 자동차 데이터를 수집한다.

 

이러한 방대한 데이터를 수집하려면 상당히 많은 시간과 노력이 필요하지만,

 

요즘은 손쉽게 사용할 수 있는 고퀄리티의 데이터셋들이 많이 있다.

 

이러한 데이터셋을 이용해서 machine learning classifier를 학습시킬 수 있다.

 

ML 알고리즘은 어떤 식으로든 데이터를 잘 요약해서 다양한 객체들을 인식할 수 있는 모델을 만들어낸다.

 

그리고 만들어진 모델로 새로운 이미지를 테스트하면 고양이인지 강아지인지 등 객체를 잘 인식할 수 있다.

 

이러한 관점으로 보면 만들려는 API는 위의 그림처럼 변할 수 있다.

 

하나는 train 함수이다. 입력은 이미지와 해당 레이블이고 출력은 학습 모델이 된다.

 

또 다른 하나는 predict 함수이다. 입력이 학습 모델과 테스트 이미지이고 출력은 예측 레이블이 된다.

 

이는 machine learning의 key insight이다. 이러한 key insight는 지난 10-20년간 아주 잘 동작했다.

 

data-driven approach는 deep learning 뿐만아니라 아주 일반적인 개념이다.

 

심플한 classifier를 한번 살펴보자.

 

 

 

NN 알고리즘은 아주 심플하다.

 

train 단계에서는 모든 학습 데이터를 기억하는 일만 한다.

 

predict 단계에서는 새로운 이미지가 입력되면

 

새로운 이미지와 기존의 학습 데이터를 비교해서

 

가장 유사한 학습 이미지의 레이블로 출력한다. 아주 심플하다.

 

좀 더 구체적으로 살펴보기 위해 CIFAR-10 데이터셋을 살펴보자.

 

 

 

CIFAR-10은 ML에서 자주 쓰이는 테스트용 데이터셋이다.

 

비행기, 자동차, 새, 고양이 등 총 10가지 클래스가 있다.

 

10가지 각 카테고리가 있고 총 50,000장의 학습용 이미지가 있다.

 

50,000장의 학습용 이미지는 각 카테고리에 균일하게 분포되어 있다.

 

10,000장의 테스트 이미지도 존재한다.

 

위 그림의 오른쪽에서 맨 왼쪽 열은 테스트 이미지이다.

 

그의 오른쪽 방향으로는 학습 이미지들 중 테스트 이미지와 유사한 순서대로 정렬된 이미지이다.

 

테스트 이미지와 학습 이미지를 비교해보면, 눈으로 보기에는 상당히 비슷해보인다.

 

참고로 이미지는 32x32로 상당히 작다.

 

두 번째 행의 이미지는 흰색 강아지이다. 그리고 그 오른쪽으로 가장 가까운 이미지도 강아지를 나타낸다.

 

하지만, 두번째, 세번째 등 그 오른쪽들을 보면 사슴이나 말과 같아 보이는 이미지들도 존재한다.

 

강아지는 아니지만 이미지 중간에 흰색 객체가 있는 등의 눈으로 보기에도 비슷한 경향을 보인다. 

 

이렇든 NN 알고리즘은 학습 데이터셋에서 가장 가까운 샘플을 찾게 된다.

 

이렇게 찾은 샘플의 레이블 또한 알 수 있다.

 

왜냐하면 찾은 샘플 데이터는 학습 데이터이기 때문에 레이블을 미리 알고 있다.

 

NN 알고리즘이 잘 동작하지 않을 것 같지만, 그럼에도 불구하고 해볼만한 좋은 예제라고 할 수 있다.

 

 

 

여기에서 중요한 점은 이미지가 쌍으로 존재할 때 어떻게 비교할 것인가 이다.

 

테스트 이미지 하나를 모든 학습 데이터와 비교할 때 여러가지 비교 방법들이 있다.

 

정확하게 말하면 '어떤 비교 함수를 사용할지'에 달려있다.

 

위의 그림에서는 L1 distance를 사용했다. Manhattan distance라고도 한다.

 

이미지를 pixel-wise로 비교한다. 예를 들어 4x4 테스트 이미지에서

 

학습 이미지의 같은 자리의 픽셀을 서로 빼고 절대값을 계산한다.

 

이렇게 픽셀 간 차이를 계산하고 모든 픽셀의 수행 결과를 모두 더한다.

 

image classification 문제에서 이러한 방법은 별로일 것 같지만 연습삼아 해보는것이 좋다.

 

위의 예제에서는 두 이미지간의 차이는 '456' 을 나타낸다.

 

 

 

NN classifier를 구현한 python 코드는 짧고 간결하다.

 

numpy에서 제공하는 vectorized operations를 이용했기 때문이다.

 

train 함수의 경우 위에 언급한대로 단지 학습 데이터를 기억하는 일만 한다.

 

predict 함수에서는 테스트 이미지를 입력받고 L1 distance로 비교한다.

 

학습 데이터들중에 테스트 이미지와 가장 유사한 이미지를 찾는다.

 

이 간단한 classifier에 대한 몇 가지 궁금증이 생길 수 있다.

 

첫번째, 학습 데이터셋의 이미지가 총 N개라면 train/predict(test) 함수의 속도는 어떻게 될까?

 

일단 train time은 상수시간 O(1)이다. 데이터만 기억하면 되기 때문이다.

 

포인터를 잘 이용해서 복사를 하게 되면, 데이터 크기에 관계없이 상수시간으로 끝낼 수 있다.

 

하지만 test time은 N개의 학습 데이터 전부를 테스트 이미지와 비교해야만 한다. 상당히 느린 작업이다.

 

이는 우리가 기대하는 것과 다르다 (train time < test time)

 

우리는 train time은 조금 느려도 되지만 test time은 빠르길 원한다.

 

예를들어 어떤 classifier를 학습시키고 있다고 생각해보면

 

좀 더 좋은 성능을 얻기 위해 train time에 많은 시간을 쏟을 수 있다.

 

classifier는 test time 관점에서 생각해보면 

 

이 모델이 휴대폰이나, 브라우저 등 low power device에서 동작해야 할 수도 있다.

 

이러한 상황에서는 classifier가 test time에서 빠른 성능을 보장할 수 있어야 한다.

 

이런 관점에서 NN 알고리즘은 정반대의 경우이다.

 

CNN과 같은 parametric model들은 NN과 정반대이다.

 

train time은 엄청 오래 걸릴지 모르나 test time은 엄청 빠르다.

 

 

 

그렇다면 NN 알고리즘을 실제로 적용해 본다면 어떻게 생겼을까?

 

위의 그림은 NN 알고리즘의 'decision regions'을 나타낸다.

 

2차원 평면 상의 각 점은 학습 데이터이다. 점의 색은 클래스 레이블(카테고리)이다.

 

위의 예제에서는 클래스가 5개이다.

 

차원 평면 내의 모든 좌표에서 각 좌표가 어떤 학습 데이터와 가장 가까운지 계산한다.

 

그리고 각 좌표를 해당 클래스로 분류한다.

 

하지만 이 classifier는 그다지 좋지 않다.

 

예를들어 가운데를 보면, 대부분 초록색 점들인데 중간에 노란 점이 껴있다.

 

NN 알고리즘은 '가장 가까운 이웃' 만을 보기 때문에, 녹색 무리 한 가운데 노란색 영역이 생겨 버린다.

 

사실은 노란색이 아닌 초록색 영역이여만 한다.

 

이와 비슷하게 근처에 초록색 영역이 파란색 영역을 침범하고 있다.

 

이는 잡음(noise)이거나 가짜(spurious)일 수 있다.

 

이러한 문제들이 발생하기 때문에 NN의 좀 더 일반화된 버전인 k-NN 알고리즘이 탄생했다.

 

 

 

단순하게 가장 가까운 이웃만 찾는것이 아닌 distance metric을 이용해서 가까운 이웃을 K개 만큼 찾고,

 

이웃끼리 투표하는 방법이다. 그리고 가장 많은 표를 획득한 레이블로 예측한다.

 

투표 방법들도 거리별 가중치를 고려한다거나 다양하게 존재하지만

 

가장 잘 동작하면서 쉬운 방법은 득표수만 고려하는 방법이다.

 

위의 세개의 예제는 동일한 데이터를 사용한 K-NN 분류기들이다.

 

각각 K=1, 3, 5에서의 결과이다.

 

K=3을 보면 초록색 영역에서 자리 잡았단 노란색 영역이 깔끔하게 사라진 것을 볼 수 있다.

 

왼쪽의 빨강/파랑 사이의 뾰족한 경계들도 점차 부드러워지는 것을 볼 수 있다. 다수결의 힘이라고 볼 수 있다.

 

K=5를 보면 파란/빨간 영역의 경계가 부드럽고 좋아졌다.

 

대체 NN 분류기를 사용하면 K는 적어도 1보다는 큰 값을 사용한다.

 

왜냐하면 K가 1보다 커야 decision region가 더 부드러워지고 더 좋은 결과를 보이기 때문이다.

 

 

 

이미지 분류를 다루는 문제에서 K-NN을 사용하는 전략은 그다지 좋은 방법이 아니다.

 

cifar-10에서 K-NN을 사용한 결과이며, 잘 분류된 것은 초록색, 아닌것은 빨간색으로 표기하였다.

 

성능이 별로 좋지 않다.

 

K값을 높이면 어떻게 될까? 가장 가까운 이웃 뿐만 아니라 top3, top5 혹은 모든 행(row)을 사용하면 어떻게 될까?

 

더 많은 이웃들이 투표에 참여하면 각종 잡음에 조금 더 강인해질 것으로 추측할 수 있다.

 

 

 

K-NN을 사용할 때 결정해야 할 사항이 한 가지 있다. 서로 다른 점들을 어떻게 비교할 것인가이다.

 

지금까지는 L1 distance를 사용했다. 픽셀 간 차이의 절대값의 합이다.

 

하지만 L2 distance, Euclidean distance를 사용할수도 있다. 픽셀간 차의 제곱의 합의 루트를 거리로 이용하는 방법이다.

 

어떤 거리 척도(distance metirc)을 선택할 지는 흥미로운 주제이다.

 

왜냐하면 서로 다른 척도에서는 해당 공간의 근본적인 기하학적 구조 자체가 서로 다르기 때문이다.

 

 

 

어떤 거리 척도를 사용하는지에 따라 실제 기하학적으로 어떻게 변하는지 위의 그림을 통행 알 수 있다.

 

모두 동일한 데이터를 사용했다. 단지 왼쪽은 L1 distacne, 오른쪽은 L2 distance를 사용했다.

 

결과를 보면 거리 척도에 따라 결정 경계의 모양 자체가 달라짐을 알 수 있다.

 

 

 

어떻게 하면 주어진 문제와 데이터에 꼭 맞는 모델을 찾을 수 있을까?

 

K-NN에서 K와 거리척도를 '하이퍼파라미터'라고 한다.

 

하이퍼파라미터는 train time에 학습하는 것이 아니기 때문에 학습 전 사전에 반드시 선택해야 한다.

 

데이터로 직접 학습시킬 방법이 없다.

 

(음 하이퍼파라미터도 학습을 통해 최적을 구하는 논문이 있는것으로 알고 있다,

근데 요즘 논문이나 코드들을 보면 아직까지 메뉴얼하게 정하는거 보면 딱히 효율이 없는거 같기도)

 

하이퍼파라미터를 정하는 일은 문제 의존적(problem-dependent)이다.

 

가장 간단한 방법은 데이터에 맞게 다양한 하이퍼파라미터 값을 시도해 보고 가장 좋은 값을 찾는 것이다.

 

단지 여러가지 시도를 해보고 좋은 것을 선택하는 것이다.

 

하지만 하이퍼파라미터 값들을 실험해 보는 작업도 다양하다.

 

'다양한 하이퍼파라미터를 시도해 보는 것'과

 

'그 중 최고를 선택하는 것'은 어떻게 할까?

 

 

 

가장 먼저 떠올릴 수 있는 아이디어는 매우 단순하다.

 

'학습 데이터의 정확도와 성능'을 최대화하는 하이퍼파라미터를 선택하는 것이다.

 

이 방법은 정말 끔직한 방법이다. 절대로 이렇게 해서는 안된다.

 

예를 들어 NN 분류기에서 K=1일때 학습 데이터를 가장 완벽하게 분류한다.

 

학습 데이터의 정확도와 성능 측면에서 K=1일때가 최고이기 때문이다.

 

하지만 앞서 보았듯이 실제 K를 더 큰 값으로 선택하는 것이 학습 데이터에서는 몇 개 잘못 분류 할 수 있겠지만,

 

학습 데이터에 없던 테스트 데이터에 대해서는 더 좋은 성능을 보일 수 있다.

 

궁극적으로 기계학습에서는 학습 데이터를 얼마나 잘 분류하는지는 중요하지 않다.

 

우리가 학습시킨 분류기가 한번도 본 적 없는 데이터를 얼마나 잘 예측하는지가 중요하다.

 

그렇기 때문에 학습 데이터에 대해서만 정확도와 성능을 신경쓰는 것은 최악이다.

 

또 다르게는, 전체 데이터셋 중 학습 데이터를 쪼개서 일부를 테스트 데이터로 사용하는 것이다.

 

학습 데이터로 다양한 하이퍼파라미터 값들을 학습을 시키고

 

테스트 데이터로 적용시킨 다음, 하이퍼파라미터를 선택하는 방법이다.

 

이 방법이 좀 더 합리적인 방법 같지만, 이 또한 쓰면 안되는 방법이다.

 

기계학습은 궁긍적으로 한번도 보지 못했던 데이터에서 잘 동작해야한다.

 

하지만 학습시킨 모델 중 테스트 데이터에만 가장 잘 맞는 모델을 선택한다면

 

이는 그저 가지고 있는 테스트셋에서만 잘 동작하는 하이퍼파라미터를 고른 것일수 있다.

 

좀 더 일반적인 방법은 데이터를 세 개로 나누는 것이다.

 

데이터의 대부분을 트레이닝셋, 일부는 밸리데이션셋, 일부는 테스트셋으로 나눈다.

 

그리고 다양한 하이퍼파라미터를 트레이닝셋으로 학습시킨다.

 

그리고 벨리데이션셋으로 검증한다. 그리고 벨리데이션에서 가자 좋았던 하이퍼파라미터를 선택한다.

 

최종적으로 개발/디버깅 등 모든 일을 마친 후에 밸리데이션셋에서 가장 좋았던 분류기를 가지고

 

테스트셋에서는 오직 한번만 수행한다.

 

이 마지막 수치가 논문과 보고서 등에 삽입되는 것이다.

 

실제로 벨리데이션 데이터와 테스트 데이터를 엄격하게 나눠놓는 것은 상당히 중요하다.

 

 

 

또 다른 하이퍼파라미터 선택 전략은 교차 검증(cross-validation)이다.

 

이 방법은 작은 데이터셋일 경우 많이 사용하고, deep learning에서는 많이 사용하지는 않는다.

 

교차 검증은 우선 테스트 데이터를 정해 놓는다. 이는 마지막에만 사용된다.

 

그리고 나머지 데이터를 트레이닝/벨리데이션으로 딱 나눠놓는 대신에

 

위의 그림처럼 트레이닝 데이터를 여러 부분으로 나눈다.

 

이런 식으로 번갈아가면서 벨리데이션셋을 지정해준다.

 

위의 그림은 5-Fold cross-validation을 사용하고 있다.

 

처음 4개의 fold에서 하이퍼파라미터를 학습시키고 남은 한 fold에서 알고리즘을 평가한다.

 

그리고 1, 2, 3, 5 fold에서 다시 학습시키고, 4 fold로 평가한다. 이런식으로 계속 순환한다.

 

이를 방식을 통해 최적의 하이퍼파라미터를 확인할 수 있다.

 

이런 방식이 거의 표준이긴 하지만 실제로 deep learning과 같은 큰 모델에서 학습시킬 때는

 

학습 자체가 계산량이 많기 때문에 실제로는 잘 쓰지 않는다.

 

(coco dataset으로 cross-validation한다고 생각하면 끔직하다)

 

 

 

위의 그래프는 5-fold 교차 검증을 수행한 결과이다. x축은 K-NN의 K이다. y축은 분류 정확도이다.

 

각 K마다 5번의 교차 검증을 통해 알고리즘이 얼마나 잘 동작하는지 보여준다.

 

'테스트셋이 알고리즘 성능 향상에 미치는 영향'을 알아보려면 K-fold 교차검증이 도움이 될 수 있다.

 

여러 validation fold 별 성능의 분산(variance)을 고려할 수 있다.

 

분산을 같이 계산하게 되면, 어떤 하이퍼파라미터가 가장 좋은지 뿐만 아니라, 그 성능의 분산도 알 수 있다.

 

하이퍼 파라미터에 따라 모델의 정확도와 성능을 평가할 수 있다.

 

그리고 벨리데이션셋의 성능이 최대인 하이퍼파라미터를 선택하게 된다.

 

위의 그림에서는 K=7인 경우에 가장 좋은 성능을 나타낸다.

 

 

 

하지만 실제로 입력이 이미지인 경우에는 k-NN 분류기는 잘 사용하지 않는다.

 

앞서 말한 문제들 때문이다.

 

한가지는 너무 느리기 때문이다.

 

또 하나는 L1/L2 거리척도가 이미지들간의 거리를 측정하기에는 적절하지 않다는 점이다.

 

이 벡터간의 거리 측정 관련 함수들은 이미지들 간의 '지각적 유사성'을 측정하는 척도로는 적절하지 않다.

 

위의 그림을 보면 원본 이미지와 세개의 왜곡된 이미지를 볼 수 있다.

 

눈과 입을 가리거나, 픽셀을 이동시키거나, 파란색 색조를 추가한 것이다.

 

이 왜곡된 이미지들과 원본과의 L2 distance를 측정해보면 모두 동일하게 계산된다.

 

이는 L2 distance가 이미지들간의 '지각적 유사도'를 측정하기에는 적합하지 않다는 의미가 된다.

 

 

 

k-NN의 또 다른 문제 중 하나는 '차원의 저주'이다.

 

k-NN은 학습 데이터를 이용하여 공간을 분할했다.

 

이는 k-NN이 잘 동작하라면 전체 공간을 조밀하게 커버할 만큼의 충분한 학습 데이터 샘플이 필요하다는 것을 의미한다.

 

그렇지 않다면 이웃이 엄청 멀 수도 있으며, 그렇게 된다면 테스트 이미지를 제대로 분류할 수 없을 것이다.

 

공간을 조밀하게 구성하려면 충분한 양의 학습 데이터가 필요하고

 

그 양은 차원이 증가함에 따라 기하급수적으로 증가한다.

 

이는 아주 좋지 않은 현상이다. 기하급수적으로 증가하는 것은 언제나 옳지 못하다.

 

위의 그림에서 각 점은 학습 데이터 샘플을 의미한다. 점 하나하나가 학습 샘플이다.

 

각 점의 색은 학습 샘플이 속한 카테고리를 나타낸다.

 

맨 왼쪽 1차원 공간을 조밀하게 덮으려면 학습 샘플 4개면 충분하다.

 

2차원 공간을 다 덮으려면 16개가 필요하다. 1차원의 4배이다.

 

이렇게 3, 4, 5차원 같이 고차원을 고려해보면 각 공간을 조밀하게 덮기 위한 필요한 학습 샘플 수는

 

차원이 늘어남에 따라 기하급수적으로 증가하게 된다.

 

linear classifier는 간단한 알고리즘이다. 아주 중요하고 NN과 CNN의 기반이 되는 알고리즘이다.

 

어떤 사람들은 NN를 레고 블럭에 비유한다.

 

NN을 설계할 때 다양한 컴포넌트를 사용할 수 있다.

 

이 컴포넌트들을 모아서 CNN이라는 거대한 타워를 지을 수 있다.

 

앞으로 보게 될 다양한 종류의 딥러닝 알고리즘들의 가장 기본이 되는 블록 중 하나가 바로 linear classifier이다.

 

그렇기 때문에 linear classifier가 어떻게 동작하는지 정확히 이해하는것이 아주 중요하다.

 

왜냐하면 linear classifier가 결국은 전체 NN을 아우르게 될 것이기 때문이다.

 

위의 그림은 NN의 구조적인 특성을 설명하는 image captioning 예시이다.

 

image captioning에서는 입력이 이미지이고, 출력이 이미지를 설명하는 문장이 된다.

 

이미지를 인식하기 위해 CNN을 사용한다.

 

그리고 언어를 인식하기 위해 RNN을 사용한다.

 

이렇게 두 개(CNN+RNN)을 레고 블록처럼 붙이고 한번에 학습시킨다. 그렇게 되면 이런 어려운 문제도 해결할 수 있다.

 

여기서 중요한 점은 NN이 레고 블록과 같다는 것이고 linear classifier가 기본 블록이 된다는 것이다.

 

cifar-10을 다시 상기시켜보자.

 

50,000장의 학습 데이터, 10,000장의 테스트 데이터가 있고,

 

각 이미지는 32x32 픽셀을 가진 3채널 컬러 이미지이다.

 

linear classifier에서는 k-NN과는 조금 다른 접근 방법을 이용한다.

 

linear classifier는 'parametric model'의 가장 단순한 형태이다.

 

parametric model은 두 개의 요소가 있다.

 

위의 그림을 보면 입력으로 고양이 이미지가 있다.

 

이 입력 이미지를 보통 'X'로 표현한다.

 

파라미터, 즉 가중치는 문헌에 따라 다르지만 'W'라고도 하고 세타(theta)라고도 한다.

 

이제 어떤 함수 F를 만들어야 하는데, 이 함수는 입력을 X와 W로 하고, 10개의 숫자를 출력으로하는 함수이다.

 

10개의 숫자는 cifar-10의 각 카테고리별 스코어가 된다.

 

예를 들어, '고양이'의 스코어가 높다는 건 입력 X가 '고양이'일 확률이 크다는 것을 의미한다.

 

앞의 k-NN은 이러한 파라미터가 없었다.

 

단순히 전체 학습 데이터셋을 기억하고, 모든 학습 데이터셋을 predict에 사용했다.

 

하지만 parametric approach에서는 학습 데이터셋의 정보를 요약한다.

 

그리고 그 요약된 정보를 파라미터 W에 저장한다.

 

이런 방식을 사용하면 predict(test) time에 더 이상의 학습 데이터가 필요하지 않게된다.

 

test time에서 파라미터 W만 있으면 된다.

 

이 방법은 휴대폰과 같은 low power 디바이스에서 모델을 동작시켜야할때 매우 효율적이다.

 

그렇기 때문에 딥러닝은 바로 이 함수 F의 구조를 적절하게 설계하는 일이라고 볼 수 있다.

 

어떤 식으로 가중치 W와 데이터를 조합할지 여러가지 복잡한 방법으로 고려해볼 수 있는데,

 

이 과정들이 모두 다양한 NN 아키텍처를 설계하는 과정이 된다.

 

가중치 W와 데이터 X를 조합하는 가장 쉬운 방법은 단순히 둘을 곱하는 것이다.

 

이 방법이 바로 linear classification이다.

 

f(x,W) = Wx로 아주 간단한 식이다.

 

입력 이미지는 32x32x3 이다. 이 값을 길게 펴서 column 벡터로 만들면 3,072차원 벡터가 된다.

 

이 3,072차원 column 벡터를 입력으로 10개의 카테고리에 대한 스코어가 출력되야 한다.

 

따라서 파라미터 W는 10x3,072 행렬이 되야한다.

 

X와 W를 곱하면 10개의 카테고리 스코어를 의미하는 10x1 크기의 column 벡터를 얻을 수 있다.

 

'bias' 텀이 있을수도 있다. 바이어스 텀도 10x1 column 벡터이다. 바이어스는 입력에 연결되지 않는다.

 

바이어스느 '데이터와 무관하게' 특정 클래스에 '우선권'을 부여한다.

 

예를 들면 고양이 데이터가 강아지 데이터보다 훨씬 더 많거나 하는

 

데이터의 불균형한 상황에서 

 

고양이 클래스에 해당하는 바이어스가 더 커지도록 학습된다.

 

입력을 2x2 이미지라고 가정해보자.

 

linear classifier는 2x2 이미지를 입력으로 받고, 이를 column 벡터로 길게 펼친다.

 

위의 예제에서는 고양이, 강아지, 배 이렇게 3개의 클래스만 있다고 가정했을때,

 

가중치 W의 행렬은 4x3 행렬이 된다.

 

추가적으로 3차원 바이어스 벡터가 있다. (1.1, 3.2, -1.2) 

 

바이어스는 데이터와 독립적으로 각 카테고리와 연결된다.

 

고양이 스코어는 입력 이미지의 픽셀 값들과 가중치 W 행렬을 내적(inner product)한 값에 바이어스 텀을 더한 것이다.

 

이러한 관점에서 linear classification은 템플릿 매칭과 거의 유사하다.

 

가중치 행렬 W의 각 행은 각 이미지에 대한 템플릿으로 볼 수 있으며,

 

해당 row 벡터와 이미지의 column 벡터간의 내적을 계산한다.

 

여기서 내적이란 결국 클래스간 템플릿의 유사도를 측정하는 것과 비슷하다.

 

바이어스는 데이터 독립적으로 각 클래스에 scaling offset을 더해주는 것이다.

 

템플릿 매칭 관점에서 linear classification을 해석해보자.

 

가중치 행렬 W의 하나의 행을 뽑아서 이를 이미지로 시각화 시켜보면

 

linear classifier가 이미지 데이터를 인식하기 위해 어떤 일을 하는지 짐작할 수 있다.

 

위의 그림은 linear classifier가 cifar-10 이미지를 학습하고

 

가중치 행렬 W의 각 행 벡터를 시각화시킨 그림이다.

 

맨 왼쪽 이미지는 비행이 클래스에 대한 템플릿 이미지이다.

 

하늘과 같이 푸른끼가 많고 가운데에는 어떤 객체가 있는것 같다.

 

이 이미지를 해석해보자면 linear classifier가 비행기를 분류할 때 푸른색인것들을 찾고 있다고 볼 수 있다.

 

이러한 특징들이 비행기를 더 잘 찾을 수 있다고, 가중치 W가 학습했다고 볼 수 있다.

 

하지만 linear classifier의 문제 중 하나는 각 클래스에 대해서 단 하나의 템플릿만을 학습한다는 것이다.

 

한 클래스 내에서 다양한 특징들이 존재할 수 있지만, 이 모든 것들을 평균화 시키기 때문에

 

다양한 모습들이 있더라도 각 카테고리를 인식하기 위한 템플릿은 하나 밖에 없다.

 

말을 분류하는 템플릿을 보면 또 다른 문제를 볼 수 있다.

 

바닥은 초원같이 초록빛을 띄고 있다. 보통 말이 풀밭에 있으니 템플릿이 배경을 초록빛으로 학습한 것이다.

 

그런데 잘 보면 왼쪽, 오른쪽 각각 말 머리가 두 개인것을 볼 수 있다.

 

머리가 두 개인 말은 존재하지 않는다.

 

하지만 linear classifier는 템플릿이 하나밖에 허용되지 않으므로 위의 그림이 최선인 것이다.

 

그래도 NN와 같은 복잡한 모델이라면 조금 더 정확도를 높힐 수 있을 것이다.

 

클래스당 하나의 템플릿만을 학습할 수 있다는 것과 같은 제약조건이 없을 경우라면 말이다.

 

linear classifier를 또 다른 관점에서 해석할 수 있다.

 

이미지를 고차원 공간의 한 점으로 보는 것이다.

 

linear classifier는 각 클래스를 구분하는 선형 결정 경계를 그어주는 역할을 한다.

 

맨 왼쪽 비행기의 예를 보자.

 

linear classifier는 파란색 선을 학습해서 비행기와 다른 클래스를 구분할 수 있다.

 

임의의 값으로 초기화된 가중치 W가 데이터를 잘 분류하려고 학습되는 모습을 보면 아주 재밌다.

 

하지만 이미지가 고차원 공간의 하나의 점이라는 관점에서 해석해보면

 

linear classifier가 직면할 수 있는 문제가 있다.

 

linear classifier를 망칠 수 있는 예제를 만드는 것은 간단하다.

 

맨 왼쪽 그림을 보면,

 

파란색 카테고리는 0보다 큰 픽셀의 개수가 홀수인 경우이다. ([3, -1]이면 0보다 큰 수 : 3 (1개, 홀수) -> 파랑)

 

빨간색 카테고리는 0보다 큰 픽셀의 개수가 짝수인 경우이다.

 

좌표 평면에 이와 같은 규칙으로 그리면 두 개의 사분면은 파란색,

 

또 다른 두 개 사분면은 빨간색 클래스를 볼 수 있다.

 

이 데이터들을 선 하나로 분류할 수 있는 방법은 없다.

 

linear classifier로 풀기 힘든 문제이다.

 

픽셀의 수를 세는 것이 아닌, 사람의 수가 홀수/짝수인지 분류하는 문제도 동일하게 적용된다.

 

linear classifier로 풀기 어려운 또 하나의 문제는 맨 오른쪽 그림의 multimodal 문제이다.

 

위의 말 머리 두개의 예시처럼 왼쪽 머리가 하나의 파란색 원처럼 될 수 있고,

 

오른쪽 머리가 또 하나의 파란색 원처럼 될 수 있다.

 

이러한 경우에도 선을 하나만 그어서는 클래스를 분류할 수 없다.

 

multimodal data라면 한 클래스가 다양한 공간에 분포할 수 있으며,

 

이러한 문제는 linear classifier로는 풀 수 없다.

 

지금까지 linear classifier 수식을 살펴보았다.

 

linear classifier가 단순히 행렬과 벡터의 곱의 형태라는 것을 알 수 있었다.

 

템플릿 매칭 관점에서 해석해보면 각 카테고리에 대해 하나의 템플릿을 학습한다는 것을 알 수 있었다.

 

그리고 가중치 행렬 W를 학습시키면 새로운 테스트 데이터에도 스코어를 계산할 수 있다.

 

우리는 아직 가중치 행렬 W를 어떻게 학습하는지 배우지 않았다.

 

단지 linear classifier가 어떻게 구성되어 있고, 어떻게 동작하는지 간단하게 살펴보았다.

CISCO의 통계자료에 따르면 인터넷 트래픽 80% 이상이 비디오 데이터임. 이미지를 제외하고 순수 비디오만 80%임.

 

이는 인터넷의 대부분의 데이터가 시각 데이터라는 것을 알 수 있음.

 

때문에 시각 데이터를 잘 활용할 수 있는 알고리즘을 개발하는 것이 중요해짐.

 

하지만 시각 데이터에 대한 이해 및 해석은 상당히 어려운 일임.

 

YouTube의 통계자료에 따르면 매초 5시간 이상의 비디오가 업로드 된다고 함.

 

이러한 비디오를 사람이 일일이 보고 분류할 수 없음.

 

그래서 자동으로 시각 데이터를 이해하고 분석하는 알고리즘을 개발하는 것이 중요함.

 

컴퓨터 비전 분야에는 다양한 분야가 존재함. 컴퓨터 비전이 우주(Universe)의 중심이라고 할 수 있음.

 

이미지의 물리학적 형성 등을 이해하려면 물리학적 현상들을 이해할 필요가 있음.

 

동물의 뇌가 어떠한 방식으로 시각 정보를 처리하는지 이해하려면 생물학이 도움이 될 수 있음.

 

그 밖에 컴퓨터 과학, 수학, 공학 등을 다루며 알고리즘 구현에 필요한 분야들임.

 

컴퓨터 비전이 아닌 비전의 태동에 대한 학설.

 

5억 4천만년 전에 지구의 대부분은 물이였고 바다를 부유하는 생물들만 존재함.

 

많이 움직이지 않았으며, 눈(eye) 같은 건 존재하지 않음.

 

하지만 동물학자들이 화석을 연구하면 천만 년이라는 짧은 시기에 생물의 종이 폭발적으로 늘어났다는 사실을 발견함.

 

앤드류 파커라는 사람이 생물들에게 눈이 생겨서 종 분화의 시기를 촉진시킨 것으로 학설 제기.

 

볼 수 있다면 훨씬 능동적으로 변할 수 있음. 도망다니거나 쫒아다니거나.

 

살아남으려면 빠르게 진화해야했음.

 

이것이 비전의 태동임. 이 후 비전은 거의 모든 동물들의 가장 큰 감각 체계로 발전함.

 

인간이 만든 공학적인 비전.

 

우리가 알고 있는 초창기 카메라는 핀홀 카메라 이론을 기반으로 함.

 

생물학적 눈으로 발전한 눈과 상당히 유사함.

 

빛을 모아주는 구멍, 카메라 뒷편에 평평한 면에서 정보를 모으고 이미지를 투영 (빛의 직진성)

 

카메라는 오늘날 가장 인기있는 센서 중 하나임.

 

생물학자들이 비전 메카니즘 연구함.

 

1959년 Hubel과 Wiesel의 연구는 인간과 동물의 비전 연구에 가장 영향력 있었으며 컴퓨터 비전에도 영감을 줬음.

 

포유류의 시각적 메커니즘에 대해 궁금해하고 고양이 뇌를 연구함.

 

시각적 메커니즘 측면에서 인간과 고양이는 비슷함.

 

고양이 두뇌 뒷편의 시각 피질에 전극을 꼽아 어떤 자극에 반응하는지 관찰함.

 

Edge가 움직이면 반응하는것을 발견함.

 

주된 발견은 시각 처리가 처음에는 단순한 구조로 시작해서 정보가 통로를 거치면서 점점 복잡해져간다는 것임.

 

60년대 초반 컴퓨터 비전 분야의 최초 박사 학위 논문 Block World.

 

눈에 보이는 객체들을 기하학적인 모양으로 단순화함.

 

이 연구의 목표는 우리 눈에 보이는 세상을 인식하고 그 모양을 재구성하는 것임.

 

1966년 MIT 여름 프로젝트 'The Summer Vision Project' 가 진행됨.

 

여기에서의 목표는 시각 시스템의 전반적인 구현을 위해 프로젝트 참가자들을 효율적으로 이용하는 것이였음.

 

이후 50년이 넘게 지났으며, '컴퓨터 비전' 이라는 분야가 MIT 여름 프로젝트에서 시작되서

 

현재 전 세계 연구자들이 비전의 근본적인 문제들을 연구하고 있음.

 

컴퓨터 비전은 아직 숙제가 많지만, 인공지능 분야에서 가장 중요하고 빠르게 성장하는 분야 중 하나임.

 

70년대에 유명한 책 한권이 나옴.

 

이 책은 비전이 무엇이라 생각하는지, 어떤 방향으로 나아가야하는지, 비전을 인식하기 위해 어떤 방향으로 알고리즘을 개발해야하는지를 다룬 책임.

 

이 책에서는 눈으로 본 '이미지'를 '최종적인 Full 3D 표현'으로 만들려면 몇 단계 과정을 거쳐야 한다고 함.

 

첫 단계는 Primal Sketch 단계로, Edges, Bars, Ends, Virtual Lines, Curves, Boundaries 등이 표현되는 과정임.

 

앞서 Hubel & Wiesel 연구와 비슷한 경향을 보임. (시각 처리 메카니즘은 초기에 Edge와 같은 단순한 구조로 시작)

 

다음 단계는 2.5D Sketch 단계로 시각 장면을 구성하는 Surfaces, Depth, Discontinuies 등이 표현되는 과정임.

 

마지막은 모든 것을 모아서 Surface and Volumetric Primitives의 형태의 계층적이고 조직화된 '최종적인 3D 모델'을 만들어냄.

 

이러한 방식은 '비전이 무엇인가' 에 대한 이상적인 사고 과정이며, 실제로 수십 년간 컴퓨터 비전 분야에 적용되어 왔음.

 

컴퓨터 비전을 처음 입문하고 나서 직관적으로 생각해볼 수 있는 방법임.

 

1970년대에 중요한 연구들로 '어떻게 해야 실제 세계를 인식하고 표현할 수 있을까' 라는 질문에서 시작됨.

 

그 당시 사용할 수 있는 데이터가 거의 없었음. 컴퓨터도 느렸고 개인용 컴퓨터는 보급전임. (미국은 대단함, 우리나라 1970년대라면...)

 

이 상황에서 컴퓨터 과학자들은 어떻게 해야 객체를 인식하고 표현할 수 있을지 고민함.

 

Stanford에서 Generalized Cylinder, SRI에서 Pictorial Structure를 제안함.

 

이들 모두 기본 개념은 '모든 객체는 단순한 기하학적 형태로 표현 가능' 이라는 것임.

 

그림과 같이 사람을 원통 모양과 주요 부위와 관절로 표현할 수 있음.

 

이러한 연구들은 수년간 다른 연구에 상당한 많은 영향을 끼침.

 

(지금 보면 별거 아니라고 생각할 수 있겠지만, 이 때 당시 상황을 대입하면 이런 생각이 대단한거라고 봄)

 

1980년대 David Lowe는 어떻게 하면 단순한 구조로 실제 세계를 재구성 및 인식할 수 있을지 고민함.

 

면도기를 인식하기 위해 lines, edges, straight lines를 조합하여 구성함.

 

60, 70, 80년대에는 컴퓨터 비전으로 어떤 일을 할 수 있을까에 대한 고민을 하던 시대임.

 

하지만 너무 어려운 문제였음.

 

그래서 컴퓨터 비전 연구자들은 객체 인식이 어렵다면 객체 분할(segmentation)이 우선적이 아닐까 하는 생각을 함.

 

객체 분할은 이미지의 각각의 픽셀을 의미있는 방향으로 군집화하는 방법임.

 

픽셀을 군집화해도 사람을 인식할 수 있을지 모르지만,

 

적어도 배경과 사람이 속한 픽셀을 가려낼 수 있었음.

 

이를 영상 분할(image segmentation)이라고 함.

 

컴퓨터 비전에서 발전 속도가 빨랐던 분야는 얼굴 인식 분야임.

 

인간에게 얼굴은 가장 중요한 분위 중에 하나임.

 

대략 1999년, 2000년대에는 '통계적 기계학습' 방법이 점차 탄력을 얻기 시작함.

 

'Support Vector Machine', 'Boosting', 'Graphical models', 초기 'Neural Network' 등이 있었음.

 

이 중 가장 큰 기여를 한 연구는

 

Paul Viola와 Michael Jones이 Adaboost를 이용해 실시간 얼굴 인식에 성공한 것임.

 

당시 2001년이였으며 컴퓨터의 성능은 엄청 느렸지만 실시간에 가깝게 얼굴 인식을 할 수 있었음.

 

그리고 5년이 지나 2006년에 Fujifilm에서 실시한 얼굴 인식을 지원하는 최초의 디지털 카메라를 선보임.

 

이는 기초 과학 연구를 실제 제품에 가장 빠르게 응용한 사례라고 할 수 있음.

 

다시 객체 인식으로 돌아가보면,

 

90년대 후반부터 2010년도까지 '특징 기반 객체 인식 알고리즘' 이 대세였음.

 

이 시절 아주 유명한 알고리즘이 David Lowe의 SIFT임.

 

위 표지판 그림을 예로, 왼쪽과 오른쪽 표지판을 서로 매칭하기는 매우 어려움.

 

카메라 앵글이 변할 수 있으며, 화각이 변하거나, 빛이 변하는 등 객체 자체가 얼마든지 변할 수 있음.

 

하지만 객체의 특징 일부는 다양한 변화에 조금 더 강인하고 불변하는 점을 발견함.

 

이와 같은 중요한 특징들을 찾아내고 다른 객체와 매칭시켜 객체 인식을 수행함.

 

이미지 전체를 매칭하는 일보다 훨씬 심플한 방법이였음.

 

이미지의 특징을 사용하게 되면서 컴퓨터 비전은 한 단계 발전할 수 있었음.

 

이미지의 특징을 잘 뽑을 수 있다면 그 특징이 단서가 되서

 

이미지가 풍경인지, 고속도로인지 알 수 있도록 장면 전체를 인식함.

 

SPM은 이미지 내의 여러 부분과 여러 해상도에서 추출한 특징을 하나의 특징 기술자(decriptor)로 표현하고

 

Support Vector 알고리즘을 적용함.

 

이러한 방식은 사람 인식에도 영향을 끼침.

 

다양한 특징들을 잘 조합해보자는 시도였음.

 

어떻게 해야 사람을 현실적으로 모델링할 수 있을지에 대한 연구가 이루어짐.

 

HoG와 Deformable Part Model.

 

(HoG: 그라디언트의 방향을 계산하고 히스토그램을 만들어서 벡터화)

(DPM: 템플릿 이미지의 HoG와 테스트 이미지의 바운딩 박스에서의 HoG를 SVM classification)

 

21세기를 맞이하면서 하나의 변곡점을 마주하게 됨.

 

사진의 품질이 점점 좋아졌으며, 인터넷과 디지털 카메라의 발전은 좋은 실험 데이터를 만들어 낼 수 있었음.

 

2000년대 초반에 컴퓨터 비전이 앞으로 풀어야 할 문제가 무엇인지 정의를 어느정도 내림.

 

그것은 바로 '객체 인식' 임.

 

Benchmark Dataset을 모으기 시작함. 객체 인식의 성능을 측정하기 위해서임.

 

그 중 하나는 VOC이며, 20개의 클래스, 클래스당 수천장, 수만장 이미지들이 있음.

 

다양한 연구 집단에서 이를 통해 자신들의 알고리즘을 테스트하고 얼마나 진보했는지 확인할 수 있었음.

 

오른쪽 표를 보면 객체 인식 성능이 꾸준히 좋아짐.

 

이 무렵에 Princeton과 Stanford에서 어려운 질문을 던짐.

 

이 세상의 모든 객체를 인식할 준비가 되어있는지.

 

또한 Graphical Model, SVM, Adaboost 같은 기계학습 알고리즘은 학습 과정에서 overfitting을 하는 것 같음.

 

원인 중 하나는 시각 데이터가 너무 복잡하다는 것임.

 

모델의 입력은 고차원 데이터이며 이를 fit하려면 더 많은 파라미터가 필요했음.

 

학습 데이터가 부족하면 overfitting이 훨씬 빠르게 발생되고 generalization이 떨어졌음.

 

이러한 동기들을 바탕으로 IMAGENET 프로젝트를 시작함.

 

구할 수 있는 모든 이미지를 담은 가장 큰 데이터셋을 만드는 것임.

 

이 데이터셋으로 모델을 학습할 수 있고 벤치마크도 할 수 있음.

 

프로젝트는 약 3년정도 걸렸음.

 

그 결과 대략 1,400만장의 이미지와 2만2천개의 클래스 카테고리를 만들어냄.

 

당시 AI 분야에서 만든 가장 큰 데이터셋이으며, 이로 인해 객체 인식은 다른 국면으로 접어들었음.

 

IMAGENET팀은 2009년 부터 국제 규모 대회를 주최함.

 

1000개의 객체 클래스, 140만장의 이미지를 엄선함.

 

이 대회의 목적은 이미지 분류 문제를 푸는 알고리즘을 테스트하기 위한 것임.

 

참가자들은 정답 후보를 총 5가지 고를 수 있으며, 5가지중 정답이 있으면 맞춘 것임.

 

위 그림은 2010년도 2015년까지의 이미지 분류 대회 결과를 보여줌.

 

2015년도의 오류율은 사람보다 낮아짐.

 

앞서 보았던 실생활에 적용하기에는 많이 부족했던 낮은 오류율이 인간의 수준까지 오기까지

 

불과 몇 년 걸리지 않음.

 

2012년이 특히 중요한 순간임. 2010년, 2011년은 약 25% 오류율을 보이다가 2012년에 16%로 거의 10%가량이 떨어짐.

 

2012년 우승한 알고리즘은 convolutional neural network (CNN) 모델임.

 

좌측 2011년도에 Lin 알고리즘은 계층적인것을 볼 수 있음.

 

특징을 뽑고, 지역 불변 특징들을 계산하고, Pooling, SPM을 거쳐서 최종 특징 기술자를 입력으로 Linear SVM을 통해 분류함.

 

2012년에는 토론토에서 Jeff Hinton 교수 연구실의 박사였던 Alex는 7 Layer CNN을 만들었음.

 

이후 매년 IMAGENET의 우승은 NN이였음.

 

이러한 추세로 CNN은 layer가 계속 깊어졌음.

 

2015년도 Microsoft Research Asia에서 Residual Netwok의 Layer는 152개임.

 

2012년 부터 CNN의 시대가 도래했고, 이후 CNN을 개선하고 튜닝하려는 많은 시도가 있었음.

 

하지만 CNN은 2012에 처음 나온것이 아니며 오래전부터 존재했음.

 

1998년 LeCun은 숫자인식을 위해 CNN을 설계함.

 

이미지를 입력으로 받아서 숫자와 문자를 인식할 수 있는 CNN을 만들었음.

 

raw pixel data를 입력으로 받아 여러 convolution layer를 거치고 sub-sampling, FC를 거치게 됨.

 

2012년 CNN 아키텍처와 상당히 비슷함. 왜냐면 90년대 LeNet 아키텍처를 참조했기 때문임.

 

그렇다면 왜 90년대 알고리즘이 21세기에 갑자기 유명해졌을까?

 

그건 여러 큰 혁신들이 있었기 때문임.

 

하나는 '계산능력', 컴퓨터의 계산속도가 매년 빨라졌음.

 

GPU의 발전도 큰 도움이 됨. 강력한 병렬처리가 가능한데

 

이는 계산집약적인 CNN 모델을 고속으로 처리하는데 안성맞춤이였음.

 

또 하나는 데이터 차이임.

 

90년대에는 학습 데이터를 구하기가 쉽지 않았음. 지금은 IMAGENET과 같은 대규모 데이터셋이 많아짐.

 

컴퓨터 비전 연구의 목적은 '사람처럼 볼 수 있는' 기계를 만드는 것임.

 

사람은 시각 체계를 통해 아주 많은 것들을 할 수 있음.

 

단지 강아지나 고양이를 찾아서 바운딩 박스를 그리는 것 이상의 일들을 할 수 있음.

 

이러한 관점에서 컴퓨터 비전 분야는 우리가 풀어야할 수 많은 도전과제와 미해결 문제가 많음.

 

픽셀 하나하나의 분류 문제(이건 최근 많이 해결된듯), 실세계를 재구성하는 3D understanding 문제(요즘에 비유하면 디지털 트윈과 비슷할듯), 행동 인식, 증강 현실, 가상 현실, 새로운 센서 등등

 

새롭고 흥미롭고 도전적임 문제를 접할 수 있음.

 

이 프로젝트는 이미지에 박스만 그리는 것이 아니라 커다란 의미론적 그래프로 표현하는 것임.

 

그래프는 객체를 식별하는 것을 넘어 해당 장면에서 객체 간의 관계, 객체의 성격, 행동 등을 나타낼 수 있음.

 

사람들은 위의 사진을 잠깐 동안만 봐도 오른쪽과 같이 긴 문장을 작성할 수 있음.

 

'잔디밭이 보이니까 야외에서 사람들이 무슨 놀이를 하는 거 같고, 두 명씩 짝지어서 노는거 같고, 뭘 던지는 거 같고 등등'

 

사람들이 사진을 좀 더 오래 볼 수 있었다면 소설이 한편 나올수도 있음.

 

외부 지식과 경험이 더해지면 끝도 없을 수 있음.

 

이처럼 이미지의 내용을 깊게 이해하는 것은 컴퓨터 비전 분야가 진정으로 추구하는 방향임.

 

컴퓨터 비전 분야에는 많은 진보가 있었지만, 아직 가야할 길은 멀고 험난함.

 

(최근 GPT-3 정도면 비벼볼만 하지 않을려나)

2018년도에 공부했던 cs231n (2017) 강의에 대해 정리 해보려고 한다.

 

기초가 중요하니까.

 

2019년도 봄 강의가 최신인거 같은데

 

강의자료만 업데이트되고 강의 비디오는 2017년도꺼를 쓰는거 같다.

 

2017년도꺼로 정리해야지.